NMR (13C, 17O), IR and Raman Studies of Poly-Nuclear Carbonyls Transition Metal Carbonyls : A DFT Application
M.L.Sehgal1, Amit Aggarwal2 and Irshad Ahmad3
1Department of Chemistry, D.A.V. College, Jalandhar-144008, India.
2Department of Natural Sciences, LaGuardia Community College of The City University of the New York, 31-10 Thomson Avenue, Long island City, 11101, New York, USA.
3Department of Biochemistry, Faculty of Life Sciences, Aligarh Muslim University, Aligarh, 202002, Uttar Pradesh, India.
Corresponding Author E-mail: irshadahmad.bio@gmail.com
DOI : http://dx.doi.org/10.13005/ojc/330201
Article Received on : March 25, 2017
Article Accepted on : April 12, 2017
DFT implemented in ADF 2012.01 was used to know about the relative spatial displacements of three/four metals and the surrounding12 terminal and bridging CO groups in 5 poly-nuclear carbonyls:[M3(CO)12],(M=Ru,Os),[Ir4(CO)12],[Fe3(CO)12] and [Rh4(CO)12]. After optimization, the software was first run using the “NMR Program” with Single Point, Default, None, Collinear, Nosym using TZP or TZ2P Basis sets leaving Unrestricted command blank to obtain the Shielding Constants (σM ,σ 13C,σ 17O), the Chemical Shifts (δ M, δ13C, δ17O), 2 diamagnetic and 4 paramagnetic contributing terms in the σ values of constituents.The k and j values of constituents were obtained from the same program by using a new Input File.There after, the software was run with Frequencies and Raman full to obtain frequencies of the normal modes of all the (3n-6) Fundamental vibration bands of the carbonyls. All the metals in the above named first three carbonyls were spatially equivalent while in the latter two carbonyls,all the metals were not equivalent.But no where, the two metals or any two COs were found to be magnetically equivalent.Excepting Ir4(CO)12 where all the12 CO groups were spatially equivalent,in other four carbonyls, CO groups were found to be two or more types spatially.The first metal and the responding spatially equivalent other metal/s possessed same k and j values. For CO groups attached to one metal and spatially equivalent CO groups attached to other spatially equivalent metal/s, k and j values of 13C nuclei possessed the same values.A perturbing metal and spatially equivalent responding metal/s along with spatially equivalent CO groups had same k and j values respectively. The study was important in four ways. Firstly,using these parameters, we could calculate quite a more number of parameters such as Effective Spin Hamiltonian (HSpin) of the metals and 13C nuclei,Coordination Shifts (Δδ13C,Δδ17O),atomic electron valence density(integrated)/ L value of 17O and charges on both the 17O and metals along with spatial displacements/stereochemical equivalencesof constituents. Secondly, we could correlate these NMR parameters with their reported IR/Raman results which lent credence to their π–acid character.Thirdly,we classified their fundamental vibration bands types into four types.Fourthly, we could arrive at some optimization and thermal parameters of carbonyls.
KEYWORDS:Chemical Shift; Shielding Tensor; Paramagnetic Tensor; Effective Spin Hamiltonian; Magnetic Equivalence
Download this article as:| Copy the following to cite this article: Sehgal M. L, Aggarwal A, Ahmad I. NMR (13C, 17O), IR and Raman Studies of Poly-nuclear Carbonyls Transition Metal Carbonyls : A DFT Application. Orient J Chem 2017;33(2). |
| Copy the following to cite this URL: Sehgal M. L, Aggarwal A, Ahmad I. NMR (13C, 17O), IR and Raman Studies of Poly-nuclear Carbonyls Transition Metal Carbonyls : A DFT Application. Orient J Chem 2017;33(2). Available from: http://www.orientjchem.org/?p=32192 |
Introduction
We had successfully applied DFT to study NMR parameters such as: Shielding Constants (σM ,σ 13C,σ 17O),Chemical Shifts (δ M, δ13C, δ17O),two diamagnetic and four paramagnetic contributing terms in the σ values of constituents,the k and j values, Effective Spin Hamiltonian (H Spin) of the metals and 13C nuclei and Coordination Shifts (Δδ13C, Δδ17O) for the 11 mononuclear [1-3] and 9 binuclear [4] carbonyls of the 1st, 2nd and 3rd transition metals. Of course, Schreckenbach et al had ,first of all, applied DFT to 13C and 17O NMR spectra to a few mono- nuclear transition metal carbonyls of the metals like M=Cr[5,6], Mo[6], W [5,6], Fe [5,7] Ru [5,7],Os [5,7] to obtain their δ, σ and bond dissociation energies.
Carbonyls such as [M2 (CO) n] {M=V, Nb;n =10-12}[15-17] which did not obey “The18 Electron Rule” were not taken up because of their doubtful stability.
But unlike the vast variety of NMR parameters of 20 mono- and bi-nuclear carbonyls studied by our group of workers [1,4],only a little had been reported on NMR studies by computational methods for poly- nuclear carbonyls as follows:
Variable temperature 13C NMR spectra of the carbonyls M3(CO)12(M = Fe, Ru, and Os) and other related compounds [18] were reported. At least three CO scrambling processes had been shown to operate in these system. Mössbauer spectroscopic studies of iron carbonyls adsorbed on γ-Al2O3 and SiO2 were carried out by Iwai et al. [19] while 1H NMR and IR spectra of ruthenium and osmium carbonyl clusters incorporating stannylene and stannyl ligands were studied by Shariff E . Kabir and his co-workers [20]. Fang [21] submitted his thesis (2012) on,“Studies of iridium carbonyl cluster complexes,”.He prepared five polynuclear iridium-germanium mixed carbonyl- phenyl complexes and studied their X-ray strucuctures and 1H NMR by applying DFT.The same properties were studied by Yuwei Kan [22] in his thesis(2013) entitled,” New ruthenium and osmium carbonyl cluster complexes with main group bridging ligands having unusual structures and bonding”.
The present study includes 5 poly-nuclear carbonyls of transition metals in their zero oxidation states as: [M3(CO)12],(M=Ru,Os), [Ir4(CO)12],[Fe3 (CO)12] and [Rh4(CO)12].The first 3 carbonyls contained only terminal CO groups while the other two possessed both terminal and bridging CO groups. All these carbonyls obeyed “The 18 Electron Rule”. The software did not work in [Co3 (CO)12].
This Manuscript Was Subdivided as follows
It would include structures of five poly-nuclear carbonyls and the explanation in the difference their NMR parameters,Spatial and Magnetic Equivalences of the three/ four metals and the 12 CO groups on the basis of their structures.
Then we would take up the calculation of Effective Spin Hamiltonian (H Spin) of the metals and the13C nuclei, the division of (3n-6) fundamental vibration bands into Vibration Symmetry Classes and their IR/ Raman activities.
Lastly, there would be a discussion on the corroboration of NMR results with the reported IR and Raman results, the higher AEVD {Atomic Electron Valence Density (integrated)/ L} and the higher negative charge on 17O of CO of metal carbonyl than 17O of CO(g) and slight increase in positive charge on the metals of the five carbonyls.
Need of the Study
The following three points necessitated the use of a software for this study.
Computational Chemistry had, hardly, been used in ascertaining the pi-acid character of the poly-nuclear carbonyls by NMR technique though such studies were reported for mono-nuclear[1] and bi-nuclear carbonyls[4].
A range of symmetries, i.e. D3h to C2v existing in equilibrium was reported for [Fe3 (CO) 12] by Cotton and Hunter[23]. But X-raysand Moss Bauer techniques have predicted only C2v symmetry for it.We would try to ascertain whether our NMR study could give a fillip to its Mossbauer studies or not. It was the Mossbauer technique which first of all confirmed C2v structure of [Fe3 (CO) 12] with two quadrupole doublets having similar isomer shifts but different quadrupolar coupling constants (1.13 and 0.13 mm s−1)[23,24].
There could occur errors in the values of the experimentally determined vibration frequencies of bands as they were affected by coupling with neighboring group vibrations.Also, ADF software could become a better choice since it calculates Raman intensities from the polaziabilitiesof Raman bands.
Importance of the Study
The values of thermal parameters like zero- point energy, moments of inertia, entropy, internal energy and heat capacity at constant volume which will be reported for the poly-nuclear transition metal carbonyls for the first time may prove helpful to the future scientists in studying their other physical properties.
Efforts will be made to exploit this technique to study Metal to LigandTransfer (MLCT) phenomenon for macro cyclic bis- and tris- complexes of 2, 2/-bipyridine and 1,10-phenanthroline ligands with transition metal ions.
Materials, Method and Experimental Details [1-3]
ADF software was installed on Windows XP platform as “ADF jobs”. A new directory was created using “File menu” of ADF jobs.After optimization of the metal carbonyl , different commands were filled into the software to obtain a number NMR and IR/Raman parameters[1,4] such as δ,σ, k,j for M,13C and17O of carbonyls,values of two diamagnetic and four paramagnetic contributributing terms which constitute σ values of these constituents along with atomic electron valence density (integrated)/ L value of 17O and charges on the17O and metals. Diamagnetic terms were named as:{a} diamagnetic core and {b} diamagnetic valence tensor while the four paramagnetic terms were called:{c} paramagnetic (b^) tensor, {d} paramagnetic (u^) tensor, {e} paramagnetic(s^) tensor and {f} paramagnetic gauge tensors.Four more parameters namely Coordination Shifts (Δδ13C,Δδ17O),Effective Spin Hamiltonian (H^)of M and13C of carbonyls, atomic electron valence density(integrated)/L value of oxygen and charges on both the oxygen and metal atoms to elucidate the relative spatial arrangements of three /four metal ions and the 12 bridging and terminal CO groups was developed.
We obtained IR/ Raman parameters by giving different commands[1-3] to the software and corroborated them with NMR parameters to ascertain the π – acid nature of carbonyls.
Results
Tables:1, 2 gave optimizationand thermal parameters respectively.Tables: 3-5 represented σ M, σ 13C and σ 17O values and their 6 contributing terms respectively.Table:6 gave total values of diamagnetic and paramagnetic terms.Tables:7 contained σ13C, δ13C, Δ δ13CT, σ 17O, δ17O, and Δ δ 17OT.Table:8 contained types of metals and Charge on each.Table:9.contained σ17O, Charges and Atomic Electron Valence Density (integrated) /L Value on oxygen.Table:10 gave ADF numbers and σ 13Cof 13C nuclei bonded to various metals.Table:11 gave Spatial Classification of Metals and COs.Table:12 gave k, j and Hspin values of species.Table:13 represented fundamental vibration bands and their classification in terms of their IR/Raman activities.Table:14 represented Total Coordination Shifts and nCO(cm1-) of [M3(CO)12] (M= Ru,Os)
Table 1: Optimization Parameters of Poly-nuclear Carbonyls
| CarbonylDipole moment (D) | Point group | Total bonding Energy* | Total Energy: X c** (LDA)** k J mol-1 | Nucleus | I |
| Ru3(CO)12(0.04) | D3h | -19692.31 | -1389956.20(-1328606.25,-61349.95) | 101Ru | 2.5 |
| Os3(CO)12(0.05) | -do- | -20795.51 | -2854950.18(-2764119.34,-90830.85) | 187Os | 1.5 |
| Ir4(CO)12(0.03) | Td | -21464.98 | -3747674.96(-3634920.32,-112754.65) | 191 Ir | 1.5 |
| Fe3(CO)12(2.97) | C2v | -19863.97 | -809510.65(-763180.82, -46329.83) | 57Fe | 0.5 |
| Rh4(CO)122.917 ) | C3v | -19891.27 | -1772474.41(-1699114.86,-73359.55) | 103 Rh | 0.5 |
*Bonding energy is computed as an energy difference between molecule and fragments**Xc contains LDA and GGA Components; both contain Exchange and Correlation parts; GGA is zero in all the three carbonyls
Table 2: Thermal Parameters of Poly-nuclear Carbonyls at 298 K
| Carbonyl | Zero Point Energy(e V) | Some Thermal Parameters | |||||||||||
| Entropy (cal mol-1K-1) | Internal Energy (Kcal mol-1) | Constant Volume Capacity (Kcal mol-1 K-1) | |||||||||||
| Trans. | Rot. | Vib. | Total | Trans. | Rot. | Vib. | Total | Trans. | Rot. | Vib. | Total | ||
| Ru3(CO)12 | 2.169 | 45.259 | 32.40 | 64.64 | 142.313 | -do- | -do- | 60.912 | 62.689 | -do- | -do- | 62.07 | 68.028 |
| Os3(CO)12 | 1.904 | 46.306 | 32.75 | 69.43 | 148.491 | -do- | -do- | 63.229 | 65.006 | -do- | -do- | 66.76 | 72.721 |
| Ir4(CO)12 | 2.211 | 46.887 | 32.o3 | 81.34 | 160.259 | -do- | -do- | 64.51 | 66.29 | -do- | -do- | 74.34 | 80.299 |
| Fe3(CO)12 | 2.229 | 44.538 | 34.11 | 72.96 | 151.628 | 0.889 | 0.889 | 63.383 | 65.161 | 2.981 | 2.981 | 68.82 | 74.787 |
| Rh4(CO)12 | 2.211 | 45.714 | 34.19 | 85.40 | 165.300 | -do- | -do- | 64.73 | 66.511 | -do- | -do- | 77.60 | 83.566 |
Table 3: σ M, Diamagnetic and Paramagnetic Contributions [p pm]
| Carbonyl a | σ M | Diamagnetic Contributions | Paramagnetic Contributions |
| {a} {b} | {c} {d} {e} {f} | ||
| Ru3(CO)12 (1) | Ru(1,2,3) -1742.1 | 4161.944 ,96.31 | 540.901,-6803.485, 265.34, -3.066 |
| Os3(CO)12 (2) | Os (1,2,3) 2823.1 | 8814.709 ,238.77 | 662.065,-6855.089, -32.966, -4.426 |
| Ir4(CO)12 (3) | Ir(1,2,3,16)1886.2 | 8956.268,264.36 | 557.80,-7660.153, -231.292, -0.782 |
| Fe3(CO)12 (4) | Fe6(1) -4798.7 | 1907.269,127.66 | -217.75,-7644.23, 1041.906 -13.58 |
| Fe7(2,3)-4293.4 | 1907.240 ,128.43 | -241.245,-6873.934,797.975, -8.813 | |
| Rh4(CO)12 (5) | Rh7(1,2,4)-753.8 | 4274.142,122.34 | -654.353,-5266.00, 775.955, -6.072 |
| Rh6(3) -630.93 | 4274.135,118.46 | -666.97 ,-5493.796, 1145.84 -8.595 |
a ADF Numbers in parentheses [Figs: 1-5]
Table 4: σ13C, Diamagnetic and Paramagnetic Contributions [p pm]
| Carbonyl a | σ 13C | Diamagnetic Contributions {a} {b} | Para magnetic Contributions {c} {d} {e} {f} |
| Ru3(CO)12(1) | C (4,6,16,18,22,24)-67.23C (8,11,12,14,21,26)-31.2 | 199.233,49.493199.233,48.692 | 2.003, -350.460, 28.805, 3.698-0.935,-307.488, 28.243 ,1.061 |
| Os3(CO)12(2) | C (5,6,8,18,20,26)-23.63C (10,12,14,16,23,24)-53.9 | 199.232,48.935199.233,50.241 | -0.117 ,-304.919, 32.923, 0.3120.742,-337.539, 29.955, 3.439 |
| Ir4(CO)12(3) | C(5,7,10,11,14,15,17,20,21,24,26,27) 5.41 | 199.232,51.388 | 0.284 , -281.927, 35.577 , 0.846 |
| Fe3(CO)12(4) | C (4,6)-120.66C (8,10) -13.01C (12,14)-39.11C (16,19,20,22) -24.0C (25,26) -1.89 | 199.223,45.460199.227,49.056199.226,49.308199.227,48.983199.225,49.238 | 3.269, -424.572, 66.024 ,-10.068-0.659 , -291.828, 31.829, -0.6351.508, -319.762, 28.437, 2.1770.102, -303.386, 30.303, 0.758-1.460 ,-275.199, 24.531, 1.778 |
| Rh4(CO)12(5) | C (5,9,27) 2.81C (8,19,21) -0.55C (11,13,15)-77.52C (17,23,25) -4.99 | 199.227,49.993199.227,51.445199.230,43.277199.226,51.082 | -0.289, -273.247, 26.856, 0.2671.083 ,-278.439, 23.921, 2.2160.541, -362.892, 44.744, -2.4200.174, -279.547, 22.862 ,1.212 |
a.ADF Numbers in parentheses [ Figs: 1-5 ]
Table 5: σ 17O, Diamagnetic and Paramagnetic Contributions [p pm]
| Carbonyl(Fig. No.) | σ 17O | Diamagnetic Contributions {a} {b} | Paramagnetic Contributions {c} {d} {e} {f} |
| Ru3(CO)12(1) | O (5,7,17,19,23,25)-192.82O (9,10,13,15,20,27)-115.5 | 269.472 ,129.954269.472 ,129.314 | 1.788 ,-539.118,-53.474,-1.439-0.397,-461.428,-51.517,-0.924 |
| Os3(CO)12(2) | O (4,7,9,19,21,27)-94.67O (11,13,15,17,22,25)-155.0 | 269.472 ,129.012269.472,129.982 | -0.104,-444.782,-46.704,-1.5781.115,-509.706,-43.737,-2.143 |
| Ir4(CO)12(3) | O(4,6,8,9,12,13,18,19,22,23,25,28) -41.57 | 269.472,130.284 | 0.341,-396.061,-44.261,-1.336 |
| Fe3(CO)12(4) | O (5,7) -468.88O (9,11) -59.35O (13,15) -117.54O (17,18,21,23) -82.34O (24,27) -38.23 | 269.467 ,133.908269.470 ,129.938269.470, 129.878269.470 ,130.174269.468 ,130.003 | 0.458,-732.984,-135.456.-4.27-0.191,-410.922,-45.114 -2.5321.129,-480.661,-35.301,-2.0510.276,-434.934,-45.182,-2.147-0.639,-396.341,-39.915,-0.803 |
| Rh4(CO)12(5) | O (6,10,28) -48.23O (7,20,22) -49.40O (12,14,16)-337.92O (18,24,26) -57.92 | 269.469,129.853269.470,129.851269.468 ,135.290269.469,130.088 | -0.150 -398.640,-46.658,-2.0970.795,-412.121,-37.601,0.205-0.471,-578.495,-158.855,-4.860.064,-409.253, -47.276,-1.014 |
![Table 6: Total Diamagnetic, Paramagnetic contributions in σ M, σ 13C and σ17 O [p pm]](http://www.orientjchem.org/wp-content/uploads/2017/04/Vol33No2_NMR_Sehg_tab6-150x150.jpg) |
Table 6: Total Diamagnetic, Paramagnetic contributions in σ M, σ 13C and σ17 O [p pm] Click here to View table |
a.ADF Numbers in parentheses [Figs: 1-5 ]
![Table 7: σ 13C, δ 13C, Δ δ 13CT, σ 17O, δ17O, and Δ δ 17OT Values [p pm] of Carbonyls](http://www.orientjchem.org/wp-content/uploads/2017/04/Vol33No2_NMR_Sehg_tab7-150x150.jpg) |
Table 7: σ 13C, δ 13C, Δ δ 13CT, σ 17O, δ17O, and Δ δ 17OT Values [p pm] of Carbonyls Click here to View table |
a. ADF Numbers in parentheses [Figs: 1-5 ] *Apply relations: 2, 3. **Calculate by relations 4 and 5
Figures:1-5 of the carbonyls would give ADF numbers which were mentioned in the tables in parentheses where ever required.
Discussion
The discussion was divided as follows:
NMR Parameters and their Relations [25]
The parameters were related with each other as follows:
For diamagnetic complexes the σ M n+,σ1H,σ13C and σ14N were equal to the sum of the values of 2 diamagnetic and
4paramagnetic terms of M n+, 1H , 13C and 14N respectively. (1)
The relation between (σ) and (δ) for carbon was given as follows:
δ13C=181.1- σ 13C (2)
δM and δ17O were numerically equal to σ M and σ17O but had reverse signs.
σ M = – δ M (3)
σ17O= – δ 17O
The parameters {δ 13C, δ17O, σ 13C, σ17O} were, then, compared with their Coordination Shifts {Δδ13C, Δδ17O} by using the following relations:
Δ δ13C = σ13C (MCO) –(- 34.44) (4)
Δ δ 17O = σ 17O (MCO) – (-129.53) (5)
The Total Coordination Shifts {Δδ13CT, Δδ17OT,} was calculated as follows:
Δδ13 CT = [{σ13C (MCO) –(- 34.44)]*Number of spatially equivalent 13C nuclei of
1st type} +[{σ 1 3C (MCO) –(- 34.44)]*Number of spatially equivalent 13C nuclei of 2nd type} + —— so on (6)
For isolated carbon,σ reference= -181.1 p pm. So,σ reference for carbon of CO (g) and the carbon of metal carbonyls should be different because the electron densities on the isolated carbon, the carbon present in CO (g) and the carbon of a metal carbonyl would be different and the terms called Coordination shifts (Δδ), analogous to Chemical shifts, were calculated with reference values.
The π- acid ligand CO should donate electron density to the metal via dative σ bond (OC → M) to increase electron density on metal. But due to a strong π back donation from the filled d orbitals of metal to energetically favorable and geometrically suitable vacant π* molecular orbitals of CO (OC ←M), electron density should be reduced on the metal to cause an increase in the electron density on CO. As σ of a nucleus was directly related to electron density, any change in the value of its σ should serve as an indicator to the change in electron density. Hence,if CO was to act as a back acceptor, σ13C of metal carbonyls should become more than σ13C of CO (g).But according to vibration (IR/Raman) spectroscopy, the π back donation of CO would causes a decrease in vCO in metal carbonyls with respect to pure CO(g){vCO= 2143 cm1- } [26].
Some of this increased electron density on carbon was also transmitted to oxygen of CO group to make their σ 17Oalso more than that that in free CO.
Relative spatial displacements of constituting species were reaffirmed from shielding constants of the M, C and O {σM, σ 13C (M CO), σ 17O (MCO)} simply by the fact that the spatially equivalent species should have same values of shielding constants along with their constituting two diamagnetic and four paramagnetic terms respectively.
Structures, NMR and IR/ Raman Parameters of Poly-Nuclear Carbonyls
Their discussion was subdivided into nine headings (4.2.1- 4.2.9) as follows:
Trends in NMR Parameters of 5 Poly-Nuclear Carbonyls
Even if the 3 or 4 metals were found to be spatially equivalent, their CO groups might possess different NMR parameters like σ13C σ 13O, δ13C δ13O.
Depending upon the geometry, even the COs attached to the same metal might differ spatially to give more than one value of σ 13C, δ13C and σ17O, δ 17O.
Of course, the spatially equivalent species were always expected to have the same values of the 2 diamagnetic and 4 paramagnetic terms which contribute to the total values of their σ parameters respectively (Tables: 3-6).
The same inference was drawn from the charges on the metal ions where the spatially equivalent metals possessed the same charges while the spatially different metals possessed different charges (Table: 8).
[M3 (CO)12] (M= Ru, Os) contained of two types of terminal (T-1; T-2) COs; six of each type (Table-10) with two sets of σ 13C, σ 17O and δ13C, δ17O values.
[Ir4 (CO)12] possessed 12 equivalents terminal (T) COs (Table-10) with the same set of values for σ 13C, σ 17O, δ13C, δ17O parameters respectively.
[Fe 3(CO) 12]and [Rh4 (CO)12]possessed both terminal and bridging COs; the terminal showed back-accepting property while bridged COs like carbonyl group, did not act as a back acceptors. So the electron density on bridging and terminal COs would differ largely to give different σ 13C and δ 13C values.
Further, bridging COs might be bonded to two different sets of Fe (0) or R h (0) to show two or more types of σ 13C, σ 17O, δ13 C, δ 17O in addition to one or more types of σM and δ M for the three/four metals which enabled us to confirm the relative spatial displacements of the three/four metals and the 12 COs around them simply from their σ and δ values.The spatially equivalent species were also expected to have the same values of two diamagnetic and four paramagnetic terms which contribute to the total values of their σ parameters.
[Fe3 (CO) 12] and [Rh4 (CO) 12] possessed two types of Fe (0) and Rh (0) respectively. The two Fe (0)were of the same type while the third belonged to a different type. Again, in [Rh4 (CO) 12], the three Rh (0)were of one type and the fourth was of differenttype because the software gave two types of each of shielding constants and the magnetic terms in these two carbonyls respectively (Tables: 3-6).Same inference was drawn from the charges on metal ions where the spatially different metals possessed different charges (Table:8).
Table: 8. Charges and Types of Metal Ions
| Carbonyl | ADF numbers of Metal Ions | Charges on Metal Ions | Types of Metal Ions |
| Ru3(CO)12 | Ru(1,2,3) | 0.2711 | 1 |
| Os3(CO)12 | Os (1,2,3) | 0.2758 | 1 |
| Ir4(CO)12 | Ir (1,2,3,16) | 0.1807 | 1 |
| Fe3(CO)12 | Fe6(1)Fe7(2,3) | 0.05370.1508 | 2 |
| Rh4(CO)12 | Rh7(1,2,4)Rh6(3) | 0.29940.4011 | 2 |
[Fe3 (CO) 12] contained five types of CO s with 5 sets of values of σ 13C, σ 17O and δ13C, δ 17O respectively .Two bridging COs (Table: 10) possessing lowest set of values of σ 13C and σ 17O (highest set of δ13 C, δ17O) respectively were of the first type. Second type consisted of four terminal COs (Table-10) with another set of values of σ 13 C, σ 17O and δ13 C, δ17O. Each one of the remaining three types of CO s (Table-10) contained two similar terminal COs with three different sets of σ 13C, σ 17O and δ13 C, δ17O values respectively.
Table 9: Atomic Electron Valence Density (integrated)/ L Value and Charges on O
| Carbonyl | ADF Numbers of O | σ 13C(MCO) | AEVD (integrated)/ L Value at O* [Average AEVD /L/O] | Charge on O**[Average Charge/O] |
| Ru3(CO)12(1) | (5,7,17,19,23,25)(9,10,13,15,20,27) | -192.80-115.50 | 6.3846.377[6.381] | -0.377-0.384[-0.381] |
| Os3(CO)12(2) | (4,7,9,19,21,27)(11,13,15,17,22,25) | -94.700-155.00 | 6.3906.385[6.388] | -0.390-0.385[-0.388] |
| Ir4(CO)12(3) | (4,6,8,9,12,13,18,19, 22,23,25,28) | -41.57 | 6.360[6.360] | -0.360[-0.360] |
| Fe3(CO)12(4) | (5,7)(9,11)(13,15)(17,18,21,23)(24,27) | -468.88-59.35-117.54-82.34-38.23 | 6.3606.3546.3556.6006.474[6.457] | -0.347-0.351-0.360-0.355-0.354[-0.354] |
| Rh4(CO)12(5) | (6,10,28)(7,20,22)(12,14,16)(18,24,26) | -48.23-49.40-337.92-57.92 | 6.34926.3566.3826.357[6.361] | -0.349-0.356-0.382-0.357[-0.361] |
*AEVD (integrated)/ L value at O=6.359 and **Charge on O= – 0.359 in uncoordinated CO (g)
Table: 10. ADF Numbers and σ 13Cof C atoms a Bonded to Metals
|
Carbonyl [ M Nos] |
Spatially Equivalent C atoms with σ 13C |
C bonded to1st metal | C bonded to2nd metal | C bonded to3rd metal | C bondedto4th metal |
| Ru3(CO)12[1,2,3] | C (4,6,16,18,22,24)= -67.23;T-1C (8,11,12,14,21,26)= -31.2; T-2 | (16,18 ) T-1(11,12) T-2 | (22,24)T-1(14,26) T-2 | (4,6) T-1(8,21) T-2 | ——– |
| Os3(CO)12[1,2,3] | C(5,6,8,18,20,26)= -23.6; T-1C(10,12,14,16,23,24)= – 53.9; T-2 | (6,8 ) T-1(10,12) T-2 | (18,26) T-1(14,16) T-2 | (5,20) T -1(23,24) T-2 | ——– |
| Ir4(CO)12[1,2,3, 16] | C(5,7,10,11,14,15,17,20,21,24,26,27) =5.41; T | (5,7,20)T | (10,14,27)T | (11,15,26) T | (17,21,24) T |
| Fe3(CO)12Fe6(1)Fe7(2,3) | C(4,6)= -120.66; BC(8,10)= -13.01;T-3C(12,14 )= -39.11;T-4C(16,19,20,22) = -24.0; T-1C(25,26) = -1.89;T-2 | (8,10,12,14)T-3,4————- | —(4,6) B(19,22) T-I(26) T-2 | —(4,6) B(16,20) T-1(25) T-2 | —————- |
| Rh4(CO)12Rh7(1,2,4)Rh6(3) | C(5,9,27)= 2.81 ; T-3C(8,19,21)= – 0.55 ; T-1C(11,13,15)= – 77.52; BC(17,23,25)= – 4.99; T-2 | (13) B—-(15) B(21) T-1(23) T-2—- | —-(11) B(15)B(19) T-1(17) T-2—- | ——————–(5,9,27) T-3 | (13) B(11) B—-(8) T-1(25) T-2— |
a. ADF Numbers in parentheses [ Figs: 1-5 ] ;T,T-1,T-2,T-3-terminal, B-bridging
[Rh4 CO)12] contained four types of COs. Three bridging COs, though bonded to two different sets of Rh (0) showed lowest but same set of σ 13C and σ 17O (highest set of δ13 C, δ17O) values and thus belonged to the same type (Table-10).Each one of the remaining three types of COs containing three similar terminal COs (Table-10) with three different sets of σ 13C, σ 17O, δ13 C, δ17 O values belonged to three different types.
Structures and Explanation of NMR Parameters of M3(CO)12{M=Ru,Os}
Their formation, reasons for change in NMR parameters and large differences in σ 13C, σ 17O, δ13 C, δ17 O values in these carbonyls, was explained as follows:
Os 3 (CO)12 {Fig:2} and its lighter analogue Ru3 (CO) 12{Fig:1} possessed D3h symmetry consisting of an equilateral triangle of Os (0) or Ru (0) respectively. Each metal was directly bonded to two more metals, two axial and two equatorial CO ligands in a six coordinate trigonal prism geometry having sp3d2 hybridization [27].The d orbitals involved in this hybridization were: n d x z, n d y z {n=4,5; M=Ru, Os} with major lobes pointing towards the vertices though not as directly as in the case of an octahedron. In the excited state, these two d orbitals on each metal being half filled would take part in forming bonds with each one of the other two metals with their respective half filled orbitals. Each one of the remaining four vacant hybrid orbitals received a lone pair of electrons from the carbon of each one of four COs to form sigma bonds.The two axial COs attached to each metal being ^,did not back accept electron cloud from the filled nd x y, n d x2– y2, n d z2 {n=4,5; M=Ru,Os}.Rather, they would lose electron density. The π* molecular orbitals of carbon of two equatorial COs were geometrically favorable and energetically suitable with the above named filled orbitals of metal to back accept electron cloud to increase the electron density.This caused the two equatorial COs to show an increase in σ13C and σ 17Ovalues.As the decrease in electron density in two axial CO s overweighed this increase by the two equatorial COs, the Total Coordination Shift was found to be negative (Tables: 7,14).The 6 axial(2 on each M) and the other 6 equatorial( 2 on each M) would make two types of terminal (T-1; T-2) COs (Table-10) in each one of the carbonyls.
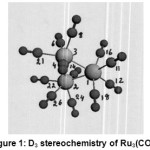 |
Figure 1: D3 stereochemistry of Ru3(CO)12 Click here to View figure |
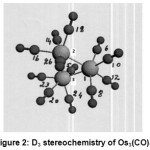 |
Figure 2: D3 stereochemistry of Os3(CO)12 Click here to View figure |
Structure and Explanation of Observed NMR Parameters in Ir4 (CO)12
Ir4(CO)12 showed a regular Td symmetry {Fig:3}; with each Ir(0) being six coordinate having sp3d2 hybridization.Three half filled hybrid orbitals of one Ir(0) overlapped with similar hybrid orbitals on each of the other three Ir(0) to form a regular tetrahedron whose each vertex was occupied by Ir (0). Each one of its remaining three vacant sp3d2 hybrid orbitals would receive a lone pair of electrons from each one of the three carbon atoms of the COs and back accept electron cloud from the three filled d orbitals of Ir (0) to form bonds with three equivalent terminals COs. The increase in electron density was indicated by the increased σ 13C and σ 17Ovalues.The 12 terminal COs were found to be spatially equivalent (Table:10) having the same σ 13C and σ 17Ovalues respectively.
 |
Figure 3: Td stereochemistry of Ir4 (CO)12 Click here to View figure |
Structure and Explanation of Observed NMR Parameters in [Fe3 (CO)12]
Although, a variety in the spatial positions of CO groups made it cumbersome to assign reasons for very large difference in σ 13C, σ 17O, δ13 C, δ17 O values in this carbonyls, yet the following points would make it easy to understand.
[Fe3(CO)12] {Fig:4;Table:10} contained two seven coordinate {Fe7(0)} and one six coordinate {Fe6(0)} iron with two bridging COs attached to both the [Fe7(0)]. The remaining ten terminal Cos were attached to all the three Fe (0).
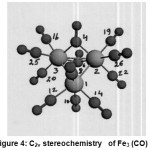 |
Figure 4: C2v stereochemistry of Fe3 (CO)12 Click here to View figure |
In the six coordinate C2v bicapped tetrahedron involving sp3d2 hybridization, two half filled d orbitals( dz2, dxz) and four empty orbitals were involved. In addition, Fe6(0) possessed three filled atomic orbitals. Each one of the two half filled sp3d2 hybrid orbital of Fe6(0) overlapped with each one of the half filled sp3d3 hybrid orbital on each of the two Fe7(0) to form two Fe6-Fe7 bonds. There were now left four vacant sp3d2 hybrid orbitals on Fe6(0). Each one would receive a lone pairs of electrons from the carbon atom of each one of four COs to form four bonds. Two axial COs being ^ to the metal did not back accept the electron cloud from the filled 3d x y, 3d y z, 3 dx2-y2 of this Fe6(0) because their symmetries were not compatible. Rather, they lost some electron density to make their σ 13C and σ 17Ovalues less than reference values (T-3).The other two COs being equatorial, back accepted electron cloud from the filled d orbitals of Fe6(0) to make their σ 13C and σ 17Ovalues more than reference values(T-4).
Each one of the seven coordinate capped octahedron involving sp3d3 (dz2, dxz, dyz) hybridization [27] possessed four half filled and three vacant hybrid orbitals.In addition, there were lying two filled atomic orbitals (dxy, dx2-y2) on Fe7(0). Three vacant sp3d3 hybrid orbitals on each one of the two Fe7 (0) formed three bonds with the three COs. Each one of these COs would back accept the electron cloud from the filled dxy orbital so that theirσ 13C and σ 17O values became more than the reference values. Of course, in one CO where the geometries and energies of the filled 3dxy of Fe7(0) andπ* of CO were compatible received back more electron cloud than the other two CO.This made two COs {one on each Fe7 (0)} to have higher σ13C and σ17Ovalues to act as terminal carbonyls (T-2) while the remaining four COs; two lying on each Fe7(0) which would act another set of four terminal carbonyls (T-1).
Two of the four half filled hybrid orbitals were then used in forming two types of M-M bonds (Fe7-Fe6 and Fe7-Fe7) with two different bond energies (65.0, 52.0 kJ mol-1) and different bond lengths {2.56, 2.68 (A0)} [28].
This would leave two half filled hybrid orbitals on each Fe7(0) unparticipating. A total of these four half filled orbitals; {two on each of the two Fe7(0) } and the two sigma lone pairs (one on each CO), then, overlapped to form four sigma bonds with two bridging COs (B) with these two Fe7(0). As the bridging COs did not back accept electron cloud, their σ 13C and σ 17Ovalues showed a decrease.
Thus this NMR study gave a fillip to Mossbauer studies (MS) of Fe3 (CO) 12. It was MS which, first of all, confirmed its C2v structure showing quadrupole doublets with similar isomer shifts but different quadrupolar coupling constants (1.13 and 0.13 (mms−1) [23,24].The software also showed the C2v point group structure for Fe3 (CO)12 .The two Fe7 (0) possessed the same values of important NMR parameters such as [σ Fe7 and δ Fe7(Tables:4 ); total diamagnetic and paramagnetic contributions(Table:6 ); charges on Metal Ions (Table:8); values of k and j (Table:12)]. In addition, both the bridging CO groups which were bonded with the two Fe7 showed the same values of their NMR parameters.
Structure and Explanation of Observed NMR Parameters in Rh4(CO)12
Again, the following points would make it easy to understand:
Rh4 (CO)12 showed C3v symmetry {Fig:5;Table:10} .Each metal was directly bonded to three more metals,i. e. there was an array of four Rh (0) with nine terminals COs and three bridging COs. Only one Rh (0) was six coordinate {Rh6 (0)} which was bonded to the remaining three Rh (0); each having coordination number seven (Rh7 (0)) to form three Rh6-Rh7 bonds. In addition, the {Rh6 (0)} was further bonded to three terminal COs. On the other hand, each one of the three Rh7 (0) was directly bonded three Rh (0) {one Rh6 (0) and two Rh7 (0)}, two terminal COs and two bridging COs as explained below:
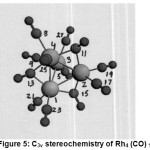 |
Figure 5: C3v stereochemistry of Rh4 (CO)12 Click here to View figure |
Rh6 (0) with sp3d2 hybridization possessed three half filled hybrid orbitals and three vacant hybrid orbitals. In addition, Rh6(0) possessed three completely filled atomic orbitals. Each one of the three half filled sp3d2 hybrid orbitals formed three Rh6 – Rh7 bonds with each one of the three other Rh7(0) by overlapping with each one of their half filled sp3d3 hybrid orbital respectively.
Each one of the remaining three vacant sp3d2 hybrid orbitals received a lone pair of electrons from carbon atom of each one of the three COs. These three COs, then, back accepted electron cloud from the three filled d orbitals of Rh6 (0) to increase the electron density which was confirmed by their increased σ13C and σ 17Ovalues.Thus the three COs acted as the terminal groups (T-3) with Rh6 (0).
Now each one of the three Rh7 (0) with sp3 d3 hybridization (having three half filled hybrid orbitals and four vacant hybrid orbitals) with two completely filled atomic orbitals was left with two half filled and two vacant sp3 d3 hybrid orbitals after forming a Rh6–Rh7 bond .Each one of the two half filled hybrid orbitals on each Rh7 (0) formed two Rh7–Rh7bonds with each of the two similar Rh7 (0).
Then, each one of the other two vacant hybrid orbitals received the lone pair from carbon of CO; back accepted the electron cloud from two filled atomic orbitals to increase the electron density as indicated by the increased σ13C and σ17Ovalues.The two terminals COs on each one of these three Rh7(0) were of two types spatially (one axial and other^).So, the 9 terminal COs were of three types.Six COs bonded to three Rh7 (0) were divided into two types of terminal COs (T-1,T-2);one T-1 and oneT-2 were bonded to each one of the three Rh7 (0)}. As already explained,three terminals Cos (T-3) were bonded to Rh6 (0).
There were still left six half filled atomic orbitals {two on each one of the three Rh7(0)} and three lone pairs of electrons on three COs which acted as bridging COs with these three Rh7(0) involving two Rh7(0) at a time.Thus, each one of three Rh7(0) was bonded to two bridging COs. Various spatial displacements of COs having different shielding constants were given in (Tables:10,11).
Table 11: Spatial Classification of Metals & CO Groups Spatial and Magnetic Equivalence of Metals and CO Groups
| Carbonyl | Types of σ M | Types of σ 13C & σ 17O | No of spatially different M & CO Ligands |
| Ru3(CO)12 | One | Two each | Metals of same type;2 types of COs; each having 6 COs |
| Os3(CO)12 | -do- | -do- | -do- |
| Ir4(CO)12 | -do- | One each | All Ir of same type; all12 COs of same type |
| Fe3(CO)12 | Two | Five each | 2 types of Fe; 2 of 1st type and one of 2nd type;5 types ofCOs;2 each of 4 types& 4 of 5th type |
| Rh4(CO)12 | Two | Four each | Two types of Rh; 3 of 1st & one of 2nd type;4 types of Co;each having 3 CO |
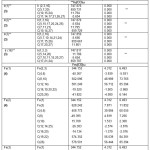 |
Table 12: k, j &H spin Values of Nuclei in Poly-nuclear Carbonyls Click here to View table |
a. ADF Numbers in parentheses [Figs:1,2,3]; *No spin- spin interaction due to large difference in % abundance of 101Ru (17.07%) and 13C (1.1%) **Large difference in γ 191Ir (0.509) and γ 13C (6.7383)
In none of these poly-nuclear carbonyls, the metals or any two COs were both spatially and magnetically equivaleni i.e.did not have same σ, δ, k and j values with other nuclei of the molecucule in addition to having same values among themselves.
The four Ir(0) and 12 COs were stereo chemically equivalent respectively.
The various spatial displacements observed for the twelve COs having different shielding constants were given in (Tables:10,11).
Calculation of Effective Spin Hamiltonian (H Spin) of M and 13C Nuclei
Spin-spin coupling parameter (j) was related to another important NMR called Effective Spin Hamiltonian (H Spin) which represented a mathematical expression to determine the energy of an NMR transition in a molecule. The world “effective” implied that its solutions reproduce the nuclear magnetic energy levels in a molecular system without reference to electrons. In a fictitious absence of surrounding electrons, the shielding constants and indirect spin-spin coupling constants would vanish leaving the NMR spectrum to be determined by Nuclear Zeeman Term and direct dipolar coupling. A simple relation to calculate Effective Spin Hamiltonian (H Spin) values of the metals and the bonded carbon atoms from their j [p pm] values as given by relation (7) and stated in [25] (Table:12)
H Spin =6.023j A B. IA. .IB. MHz mol-1 (7)
Classification of (3n-6) Fundamental Vibration Bands Into their IR and Raman Activities and the Vibration Symmetry Classes
Both IR and Raman spectra of the five poly-nuclear carbonyls were studied with their Vibration Symmetry Classes. A definite vibration symmetry symbol was given to each one of their (3n-6) fundamental vibration bands.The bands were classified as IR-active, Raman-active and both IR- and Raman-active. Some Raman- active bands which possessed negligibly small intensities or had depolarization ratios ≈0were not observed in the spectra (Table:13). Unlike their experimental determination [29-32], here the Raman intensities were calculated from the polaziabilities [33-37]and, thus, were expected to have exact values. The discussion regarding IR/Raman was divided into four parts:
The 75 bands in each of M3 (CO)12 (M= Ru,Os) were classified into symmetry symbols A1,A 2 and E having13, 12 and 50 bands respectively.So their Vibration Symmetry Class was shown as: {13A1+12A2 +25E} (Table:13; A1, A2 being singly and E being doubly degenerate).
Table: 13. Designation of IR/Raman Bands and Their Vibration Symmetry Classes
| Carbonyl | Vibration Symmetriesof bands | IR-active bands | Raman-active bands | Both IRand Ramanactive bands | IR inactive bands | May not beRaman a, b observed bands | Vibration Symmetry Class |
| [M3(CO)12](M= Ru , Os)[ D3] | A1 | —- | A1(13) | —- | A1(13) | —- | [13A1+12A2 +25E] |
| A2 | A2(12) | A2(12) | A2(12) | — | A2a (12) | ||
| E | E(50) | E(50) | E(50) | —- | —- | ||
| [Ir4(CO)12][ Td] | A1 | —– | A1(5) | —– | A1(5) | A1 b (5) | [5A1+2A2 +7E +8T1 +11T2] |
| A2 | —– | A2(2) | —– | A2(2) | A2a (2) | ||
| E | —– | E(14) | —– | E(14) | — | ||
| T1 | —– | T1(24) | —– | T1(24) | T1a(24) | ||
| T2 | T2(33) | T2(33) | T2(33) | —– | —- | ||
| [Fe3(CO)12][C2v] | A1 | A1 (24) | A1 (24) | A1 (24) | — | — | [24A1+14A2 +19B1+18 B2] |
| A2 | — | A2(14) | — | A2(14) | — | ||
| B1 | B1 (19) | B1 (19) | B1 (19) | —- | — | ||
| B2 | B2 (18) | B2 (18) | B2 (18) | — | — | ||
| [Rh4(CO)12][C3v] | A1 | A1(18) | A1(18) | A1(18) | — | [18A1 +8A2+ 26 E] | |
| A2 | —- | A2(8) | A2(8) | A2(8) a | |||
| E | E (52) | E (52) | E (52) | — |
*Numbers in parentheses indicate the bands of a specific symmetry. a. Raman active; but intensity being 10-29 to-30 ; were not observed. b. Raman active but Depolarization ratio (linear) ≈0 .0; were not observed
78 bands in Ir4 (CO)12 were classified into symmetry symbols A1, A2, E, T1 and T2, having 5, 2, 14, 24 and 33 bands respectively with Vibration Symmetry Class as: {5A1+2A2 +7E +8T1 +11T2} (Table:13;T1,T2 being triply degenerate).
75 bands in each of Fe3 (CO) 12,were classified into symmetry symbols A1,A 2, B1 and B2 having 24, 14, 19 and 18 bands respectively with Vibration Symmetry Class as: {24A1+14A2 +19B1+18 B2} (Table:13; B1,B2 being triply degenerate).
The 78 bands in Rh4 (CO) 12 were classified into symmetry symbols A1, A2 and E having 8,18, and 52 bands respectively with Vibration Symmetry Class as: {18A1 +8A2 +26 E} (Table:13 ).
Confirmation of Π–Back Acceptor Character of Carbonyls from NMR
This NMR study confirmed the π- back-acceptor nature of carbonyls in two ways:
Corroboration Betweentotal Coordination Shift (Δ Δ CT) And [nCO] Values
Since, the carbonyls possessed stereochemically different CO groups with different δC values,it would be better to correlate their [nCO] values with their Total Coordination Shift (Δ δ CT) values which were the averaged values of δC for all the carbonyl groups in any metal carbonyl.Depending upon the similarities in their symmetries, the discussion was divided into three headings as follows:
M3 (CO) 12 {M=Ru, Os}
As the Total Coordination Shift (Δ δ CT) increased, the nCO (cm-1)alsoincreased to decrease the π -back accepting capacity of electron cloud by the metals.The NMR studies corroborated well with IR studies because like nCO, the (Δ δ 13CT) values[38,39] were also found to be higher in Os3 (CO) 12 than Ru3 (CO) 12 as both possessed the same symmetry point group (D3h) (Table:14).
Ir4 (CO) 12
Since all the 12 carbonyl groups of Ir(0) were found to stereochemically equivalent; each having higher σ 13C and σ 17Ovalues(5.41and -41.57p pm) than the reference values(-34.44 and -129.53p pm) and thus confirmed the higher electron density on carbon of each carbonyl group than that on CO(g) to prove the back accepting nature of Ir4 (CO)12 with Td symmetry (Tables:4,5).
Table: 14. Coordination Shifts of [M3 (CO)12] (M= Ru, Os) Fe3 (CO)12 and M4 (CO)12
|
Carbonyl |
IR bands (cm-1){Raman bands (cm-1)} | Total Coordination Shift (Δ δ13CT )[Relation:6] | S M-M (kJ mol–1) |
d M-M (A0) |
| [Ru3(CO)12][21] | 2062, 2026, 2002,1989{2127,2034,2004,1994} | -177.3 =[(-67.23+34.44)*6+(-31.2+34.44)*6] | 78.0 | 2.85 |
| [Os3(CO)12] [21] | 2070, 2019, 1998,1986{2130,2028,2006,1989} | -51.9=[(-53.9+34.44)*6+(-23.63+34.44)*6] | 94.0 | 2.88 |
With different point group symmetries(C2v, C3v) and different number of bridging and terminal carbonyl groups,no comparison was possible in their Total Coordination Shift (Δ δ CT).
But,their π–back acceptor character was confirmed by (B) as follows:
From the Charges and AEVD Values on 17O and Metals
This NMR study proved two facts simultaneously:
Acceptance of electron density by CO groups
Since 17O became more negative(though small) than 17O of CO(g)} to show higher AEVD {Atomic Electron Valence Density (integrated)/L} than17O of CO(g) (Table:9) to confirm the acceptance of electron cloud from the metal/s.
Back donation of electron cloud by the metals
Again,each metal acquired a very small positive charge(Table:8) to prove that the metal/s would donate electron density to CO groups.
Hence like vibration spectral studies, the NMR studies also confirmed the synergic nature of the metal carbonyls.
Conclusions
We are able to reaffirm the relative spatial displacements of both the terminal and bridging carbonyl groups and the π -acid character of the carbonyls from the NMR parameters of 13C and 17O nuclei such as σ13C,σ 17O, δ13 C, δ17O along with the six diamagnetic and paramagnetic constituting terms of σM, σ13C and σ17O. We were also able to confirm the spatial equivalence/nonequivalence of the three/ four metal ions of the carbonyls.This NMR studies corroborated with the results already obtained from their IR/Raman studies. Lastly, we could identify some bands which, no doubt, were Raman active but because of their negligible Raman intensities or linear Depolarization ratios could not be observed in their Raman spectra.
References
- Sharma, S.; Chander, S.; Sehgal, M.L.; Ahmad, I. Oriental J. Chem. 2015, 31, 1417-27.
- Schreckenbach, G.; Ziegler, T. J. Phys. Chem. 1995, 99, 606-11.
- Schreckenbach, G.; Ziegler, T. Int. J.Quantum Chem. 1997, 61, 899-918.
- Sehgal, M.L.; Aggarwal, A.; Singh,S. J. App. Chem.2016, 9, 48-64.
- Li, J.; Schreckenbach, G.; Ziegler, T. J. Am. Chem. Soc. 1995, 117, 486−94.
- Li, J.; Schreckenbach, G.; Ziegler, T. J. Phys. Chem. 1994, 98, 4838−41.
- Li, J.; Schreckenbach, G.; Ziegler, T. Inorg. Chem. 1995, 34, 3245−52.
- Nicholas, J. H.; Levason, W.; Webster, M. J.Orgmet.Chem. 1998, 568, 213-23.
- Ruixue, J.; Wang,C.; Qiong,L.; Li, Q. S.; Xie,Y.; Bruce King, R.; Schaefer, H. F.III. Australian J. Chem. 2014, 67, 1318-23.
- Yi, Z.; Wang, S.; Feng, H.; Xie, Y.; Bruce King, R. Int. J. Mol. Sci. 2011,12, 2216–31.
- Xu, B.; Li, Q.S.; Xie, Y.; Bruce King, R.; Schaefer, H.F.III. Croat. Chem. Acta 2009, 82, 207-18.
- Sizova, O.V.; Varshavskii, Y.S.; Nikolskii, A.B. Russian J. Coordinat. Chem. 2005,31, 875-83.
- Qiong, L.; Li, Q.S. Chem. J. Chinese Universitie 2008, 29, 2430-34.
- Feng, X.; Gu, J.; Xie, Y.; Schaefer, H.F.III. J. Chem.Theory and Comput. 2007, 3, 1580-87.
- Ishikawa, Y.; Hacket, P. A.; Rayner, D. M. J. Am. Chem. Soc. 1987, 109, 6644.
- Tang, L.; Qiong, L,; Li, Q.S.; Xie, Y.; Bruce King, R.; Schaefer, H.F. J. Chem.Theory Comput. 2011,7, 2112–25.
- Liu, Z.; Li, Q.S.; Xie, Y.; Bruce King, R.; Schaefer, H.F.III. Inorg. Chem. 2007, 46, 1803-16.
- Forson, A.; Johnson, B.F.G.; Lewis, J.; Matheson, T. W.; Robinson, B. H.; Jackson, W.G. J. Chem. Soc. Chem. Commun. 1974, 1042-44.
- Iwai, K.; Katada, M.; Sano, H.; Iwasawa. Y. J. Radioanalyt. Nuc.Chem. 2005, 103.
- Shariff, E. K.; Raha, A. K.; Hassan, M.R.; Nicholson, B. K; Rosenberg, E.; Sharmin, A.; Salassac, L. Dalton Trans. 2008,32, 4212-19.
- Fang, F. Ph.D. Thesis, University of South Carolina 2012.
- Kan, y. Ph.D. Thesis, University of South Carolina 2013.
- Cotton, F. A.; Hunter, D. L. Inorg. Chem. Acta 1974, 11, L9.
- Cristopher, G.; Benson,G.; Long, g.; Kolis, J.W.; Shriver, D.F. J. Am. Chem. Soc. 1985, 107, 5297–98.
- Autschbach, J. Str. Bond. 2004,112,1-43.
- Nakamoto, K. 4th Edn;;Wiley- Interscience publication, N.Y. 1986, 291-98.
- Bruce King, R. Coordinat. Chem. Rev. 2004,197, 141–68.
- Braga, D.; Farrugia, L.; Grepioni, F.; Johnson, B.F.J. J. Org. Chem. 1994, 464, C39-C41.
- Chabal, Y.J.; Rayon, P.R. J. Mol .Specrosc. 1962, 8,164.
- Schrotor, S.; Bernstein, H. J. J.Mol. Spectrosc. 1964,12,1.
- Hartley, F. R.; Tunicliff, D.D.; Jones, A. A. Spectrochem. Acta. 1962,18, 579.
- Long, D. A.; Gravenor, R. B.; Milner, D.C. Trans. Faraday Soc. 1963, 59, 46-52.
- Van Gisbergen, S.J. A.; Snijders, R. J. G.; Baerends, E. J. J. Chem. Phys. 1995, 103, 9347.
- Van Gisbergen, S.J.A.; Osinga, V.P.; Gritsenko, O.V.; Leeuwen, R.V.; Snijders, R.J.G; Baerends, E. J. J. Chem. Phys. 1996,105, 3142.
- Van Gisbergen, S.J. A.; Snijders, R. J. G.; Baerends, E. J. Chem. Phys. Lett. 1996, 259, 599-604.
- Osinga, V.P.; Van Gisbergen, S.J. A.; Snijders, R. J. G.; Baerends, E. J. J. Chem. Phys. 1997,106, 5091-98.
- Van Gisbergen, S.J. A.; Kootstra, F.; Schipper, P. R. T.; Gritsenko, O. V.; Snijders, J. G.; Baerends, E. J.; Phys. Rev. A. 1998, 57, 2556 -38.
- Kishner, S.; Fitzatrick P.J.; Plowman K. R.; Butler, I. S. J. Mol. Spectrosc. 1981,74, 29-37.

This work is licensed under a Creative Commons Attribution 4.0 International License.









