A Semi-Empirical Approach for the Cohesive Energy of the Alkali Halides

Introduction

The cohesive energy of ionic compounds has been studied by many authors over the last several decades [e.g.1].  These incorporate various possible effects. As a result of the comprehensive nature of the treatments, these involve many terms. We adopt a simple semi-empirical approach with at most three terms in the expression for the cohesive energy. Instead of finding out the coefficients of these three terms from a theoretical picture, we obtain these by fitting the experimental data. A fair amount of success has been achieved.

The results of the present effort are compared with those of some of the earlier authors, with regard to the cohesive energy. For the purpose of comparing the results, it is plausibly assumed that the data may have a maximum error of 1%. On that basis, the x²/ datum is obtained for the results of all the authors considered here, including ourselves. The x² /datum is a reasonable index for the comparison, even if the error be different from 1%.

The x²  may be defined as:

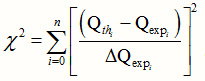
where Q_exp  is the ith experimental datum of a certain physical quantity,  Q_exp its theoretical value and  is the experimental error in the measurement of the ith quantity.

Outline of the proposed Semi-Empirical formula of the cohesive energy.

In our approach to the problem, we take Castellan’s inter-ionic potential energy function as[2]:

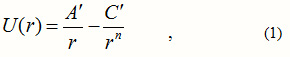
where r is the nearest neighbour distance, regarded here as a variable. The first term above is the electrostatic interaction energy and the second is the repulsive energy of the collision of the two electron clouds. This is responsible for the stability of the crystal, although it does not contribute much to the cohesive energy. The cohesive energy may be taken as the value of U(r) at the equilibrium value of this distance. Castellan uses a theoretical approach to obtain the parameters , and n. He finds n to vary from 7 to 10.5 for the halides of Li. We take  and  to be adjustable parameters and fix n to a positive integral value, say 8. We drop the dash when we take these as adjustable parameters. In this light, the cohesive energy E_c may be written , in terms of the equilibrium nearest neighbour distance r_o , as: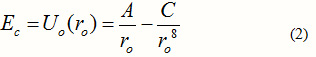

The nearest neighbour distance r_o of the alkali halides is available in the standard literature [3]. We have left out many other effects. To phenomenologically simulate these, we add an additional term, B/r_o with a negative sign, to write:

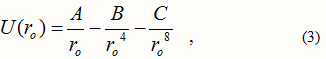
We take all the alkali halides except the Cs halides as all of these, except CsF, have a structure different from that of the rest of the alkali halides. The other authors, whose work we compare here, have done the same in this regard.

In Table-1 we reproduce the predictions of the cohesive energy of the seven authors, along with /datum, for the alkali halides. In Table-2, we give the predictions of the formula (3), when only the first term is taken, when the first and the last term are taken and when all the three terms are taken. The /datum is given , at the bottom , for all these cases.

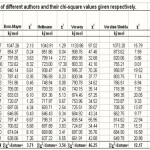Table 1 Click here to View table

 

Going back to (2) and assuming that the distance between an ion-pair, when taken out of the crystal, is nearly same as r_o, and the effective charge of all the different alkali halides is nearly same, we may write:

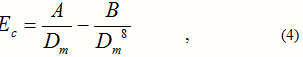
Where D_m is the electric dipole moment of the concerned alkali halide.

Both the above assumptions are not good. Yet, we take only the first term and let A have different values for the different alkalis. The results are of a qualitative nature. These are shown in Table-3. 

Discussion

We notice that the results of our formula (Table-2) are the best, when all the three terms are used, and may even be regarded as significant  because the /datum is less than unity. Even the predictions of the first term of our formula alone are tolerable. In Table-3, we give the theoretical values using the electric dipole moment i.e. using eqn. (4). These are only of a qualitative nature.

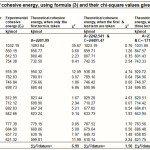Table 2: Values of cohesive energy, using formula (3) and their chi-square values given respectively. Click here to View table

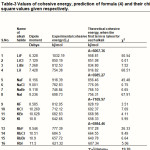Table 3: Values of cohesive energy, prediction of formula (4) and their chi-square values given respectively Click here to View table

 

In Table-4, we give the contribution of each term of our formula (3), for each of the 16 alkali halides. We find, in all the cases, that the first term, i.e. the electrostatic interaction energy between the ions, makes by far the largest contribution to the cohesive energy. The last term makes a very small contribution. The sum of the last two terms of the formula may be regarded as the cumulative effect of all the remaining contributions in the ionic crystal, other than the direct electrostatic interaction between the ions. However, it is seen from Table-4 that whereas the contribution of the second term on the R.H.S. of eqn. (3) is negative, that of the third term is positive, and is much smaller in magnitude. This suggest that , contrary to what we started with, it is plausible to regard the second term as representing the major part of the electron cloud and other repulsive contributions and the last term may be taken to represent the residual contributions from different sources.

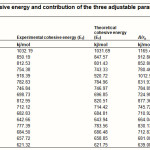Table 4: Values of cohesive energy and contribution of the three adjustable parameters given respectively Click here to View table

 

We see the contribution, arising from the last two terms of the formula is highest for the fluorides, being the highest for LiF for which it is as high as about 25% of the first terms. Then it goes down for the other fluorides, but is higher than that for  the other halides for each alkali, becoming as low as about 2% for RbI. We could not consider the chalcogenides as all the required data is not available, at present. One should not infer that our treatment is classical. We have tried to simulate the electron cloud repulsion and there is a residual term for the other things that remain. This should be adequate for a phenomenological treatment like ours. We thought there was no point in considering the three CsCl-type Cs halides for we have three data and three adjustable parameters.

Acknowledgement

Thanks are due to the Ex-Head of the department, Prof. Kishwer Saleem for extending to us the facilities of the department. We are also thankful to Prof. Sharif Ahmad, Head Chemsitry Department, Jamia Millia Islamia, New Delhi, India.

References

1. Shanker J  and Singh K , Phys. Stat. Sol. (b) 109, 411 (1982).
2. Castellan G. W. , Physical Chemistry, 3^rd edition, (Narosa Publishing House, New Delhi, 1983), pp709-713.
3. Jain V. C. and Shanker J, Indian J. Phys., 54A, 512 (1980).

---

This work is licensed under a Creative Commons Attribution 4.0 International License.