Molecular Interactions in Ternary Liquid Mixture of Morpholine, Cyclohexanone and 1-Hexanol at 308.15K and 318.15K

Introduction

Knowledge of density, viscosity and ultrasonic velocity of liquids and liquid mixtures, both binary^1-2 and ternary^3-5, is of great importance in predicting the nature of molecular interactions between unlike molecules in industrial process. Various studies have been carried out in the recent past in predicting the nature interactions^6-8 through various thermodynamic parameters. A close study of literature shows that only few work have been done using morpholine^9-11, a liquid commonly used in petrochemical industries. In the present study the nature of molecular interaction in the ternary liquid mixture involving morpholine (1), cyclohexanone¹² (2) and 1-hexanol¹³ (3) at 308.15K and 318.15K has been carried out. 

Materials and method

Morpholine (Merck, Mumbai), cyclohexanone (Merck, Mumbai) and 1- hexanol (Loba chem, Mumbai), all analar grades, were dried using suitable drying agents and distilled based on standard methods¹⁴. Ternary liquid mixtures of various compositions were prepared by mixing measured amount of pure liquids in air tight stoppered bottles of 50ml capacity. Densities of pure liquids and liquid mixtures were measured by relative density method using 10ml relative density bottle with an accuracy of ± 0.001kgm^-3. Viscosities of all pure and liquid mixtures were measured using Ostwald viscometer of 10ml capacity with an accuracy of ±0.001cP. Ultrasonic velocities of pure and liquid mixtures were measured by a single crystal variable path interferometer (Mittal Enterprises, New Delhi, Model F-80) at a frequency of 2MHz with an accuracy of ±0.02%. All the measurements were made at both 308.15K and 318.15K with the help of a digital thermostat with a temperature accuracy of ± 0.01K.

Results and discussion

The experimental densities (ρ), viscosity (η) and ultrasonic velocity (u) for the pure liquids and ternary system are presented in Table 1, 2(308.15K) and 3(318.15K).

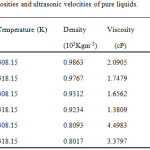Table 1: Densities, viscosities and ultrasonic velocities of pure liquids.   Click here to View table

 

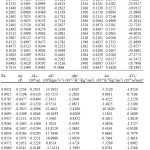Table 2: Densities, viscosities, ultrasonic velocities and acoustic parameters for the ternary mixture at 308.15K. Click here to View table

Adiabatic compressibility (Ks) has been calculated from Laplace’s equation

Ks = 1/ρu²                                                                   (1)

in which ρ and u are density and ultrasonic velocity in liquid mixture.

Acoustic impedance (Z) has been calculated by the relation¹⁵

Z= u ρ                                                      (2)

Linear free energy has been calculated by Jacobson’s relation^16,17

Lf = K/uρ^1/2                                            (3)

K is Jacobson’s constant which is temperature dependent constant but independent of the nature of the liquid.

Viscosity has been calculated using the relation

η = (At – B/t)ρ                                       (4)

A and B are constants characteristic of viscometer calculated using standard liquids water and nitrobenzene, t time of flow.

Surianarayana¹⁸ proposed a relation to calculate free volume

V_f = (M_eff u/K η)^3/2                                   (5)

K is a temperature independent constant which is equal to 4.28×10⁹ for all liquids; M_eff is effective molecular weight of the mixture calculated using the relation

M_eff = x₁M₁+x₂M₂+x₃M₃. Where x₁, x₂, x₃, M₁, M₂, M₃ are mole fractions and molar masses of the pure components 1,2 and 3.

Relative association has been calculated using the relation

Ra = (ρ/ρ₁)(u₁/u)^1/3                              (6)

Isothermal compressibility has been calculated using the relation

β_T = 1.71×10^-3/(T^4/9u²ρ^4/3)                   (7)

T is absolute temperature

Thermal expansion coefficient has been calculated using the relation

α = (0.0191β_T)^1/4                                   (8)

Excess volume (V^E) has been calculated using the relation

V^E = ((x₁M₁+x₂M₂+x₃M₃)/ρ) – (x₁M₁/ρ₁) –(x₂M₂/ρ₂) –(x₃M₃/ρ₃)        (9)

ρ₁,ρ₂and ρ₃ are densities of pure components 1,2 and 3.

Excess adiabatic compressibility (ΔKs) has been calculated from the relation

ΔKs = Ks – (φ₁Ks₁ + φ₂Ks₂ +φ₃Ks₃)                                    (10)

Ks₁, Ks₂, Ks₃ are adiabatic compressibility values of pure liquids and φ₁,φ₂ and φ₃ are volume fraction for pure liquids calculated by the relation

Φ1 =(x₁M₁/ρ₁)/(x₁M₁/ρ₁ + x₂M₂/ρ₂ + x₃M₃/ρ₃)         (11)

Excess values of other parameters are calculated using the relation

A^E = A_exp – A_id                                                                 (12)

A_id = ∑ x_i A_i   , x_i and A _i  are mole fraction and parameters of the i^th component liquid.

All the calculated excess values were fitted to Redlich – Kister¹⁹ type polynomial equation

A^E = x₁x₂x₃[a+bx₁(x₂-x₃) + cx₁²(x₂-x₃)²]                        (13)

by the method of least squares to derive the adjustable parameters a, b and c. From these a, b and c values theoretical values for all excess parameters were calculated and the standard deviation values were calculated using the relation

σ = [(A^E _exp – A^E _cal )²/(n-m)]^1/2                        (14)

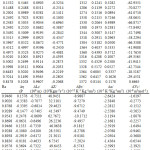Table 3 : Densities, viscosities , ultrasonic velocities and acoustic parameters for the ternary mixture at 318.15K. Click here to View table

here n is the number of measurements and m the number of adjustable parameters. The values of a, b, c and σ are given in the table 4a and 4b.

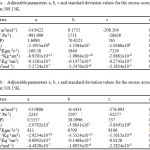Table 4a :  Adjustable parameters a, b, c and standard deviation values for the excess acoustical values at 308.15K.Table 4b :  Adjustable parameters a, b, c and standard deviation values for the excess acoustical values at 318.15K. Click here to View table

Excess volume values are negative over entire mole fraction values at 308.15K predicting the presence of strong intermolecular dipolar interaction^8,20 between the constituent liquids in the mixture. The interactions may be due to strong hydrogen bonding between 1-hexanol and morpholine, due to electron donor – acceptor complex formation nature of cyclohexanone and geometrical fitting between mixing liquids. Due to this volume contraction takes place. As temperature is raised to 318.15K negative value decreases, except at few mole fractions, that is value become more positive. Since at higher temperatures aggregates of pure liquids open up and move away thus decreasing the excess volume. The above nature of interaction is also predicted by the negative values of adiabatic compressibility and linear free energy values²¹. As the temperature is increased to 318.15K the adiabatic compressibility values becomes more negative.  The positive values of excess viscosity at higher mole fraction of morpholine indicate that flow of this mixture is difficult as compared with pure liquids⁸. Few values are negative, at lower concentration of morpholine, indicates the easy flow of the mixture at these compositions. Close perusal of the excess values of   Z, β, α, V_f, which are all negative, also predicts the presence of strong interaction between morpholine, cyclohexanone and isoamyl alcohol at all mole fractions^22-25. The Ra values are positive supporting strong interaction between constituent liquids predominating over hydrogen bonded interaction. At 318.15K all the excess values of Z, β, α, Vf  shows a similar trend, but their corresponding values decreases, predicting a decrease in the nature of interaction at higher temperatures.

Conclusion

From density, viscosity and ultrasonic velocity, related acoustical parameters and their excess values for the ternary liquid mixtures of morpholine, cyclohexanone and 1- hexanol for various mole fractions at 308.15K and 318.15K has been studied. It is found that there predominates dipole-dipole type of interaction and donor-acceptor type of complex formation in the liquid mixture.

References

1. Rosario Rajkumar X , Raman K.V.  and Arulraj S.J., Proc. Indian Acad. Sci., (Chem. Sci),90, 417 (1981)
2. Sengwa R.J., Vinita Khatri and Sonu Sankhla, Indian J. Chem., 48A, 512 (2009)
3. Thirumaran S. and Earnest Jayakumar, Indian J. Pure & Applied Phys., 47,265 (2009)
4. Venkatesu P., Basa Goud B. and Prabhakara Rao M.V., Fluid Phase Equilibria, 120,205(1996)
5. Poonam Rathore and Mukhtar Singh, Indian J. Chem., 45A, 2650 (2006)
6. Venkatesu P., Thermo Chim. Acta, 443(1), 62 (2006)
7. Ali A., J. Phy. & Chem. Liq., 38(4), 459 (2000)
8. Sharada Ghosh, Pande K.N. and Wankhade Y.D., Indian J Pure & Appl. Phy., 42, 729 (2004)
9. Pettenati C., Alessi P., Fermegila M. and Kikic I., Thermochimica Acta 162, 203 (1990)
10.  Kozin V. G. and Mukhamadiev A.A., Russian J. Applied Chem., 75 (7), 1061 (2002)
11. Akl M. Awwad, J. Chem. Eng. Data 53, 307 (2008)
12. Nikos G Tsierkezos, Ioanna E. Meolinou and Alexander C. Filippou, J. Sol. Chem., 34(12), 1371,(2005)
13.  Vasantharani P., Kalaimagal P.  and Kannappan K.N., Asian J. Appl. Sci., 2(1), 96, (2009).
14. Furnissv, Hannaford A.J., Smith P.W.G. and Tatchell A.R., “Vogel’s Text book of Practical Organic Chemistry”, 5^th ed., chap. 2, Longman, London, 165.
15. Nikam P.S.  and Hasan M., Indian J. Pure Appl. Phys., 24,502 (1986)
16. Jacobson B., Acta Chem. Scand., 6,485 (1952)
17. Jacobson B., J. Chem. Phys., 20,927 (1952)
18. Suryanarayana C.V., J. Acoust. Soc. India, 7, 107 (1976)
19. Redlich O., Kister A.T., Ind. End. Chem., 40,345 (1948)
20. Savitha Jyostna T. and Satyanarayana, Indian J. Chem., 44A, 1365 (2005)
21. Rama Rao G.V., Viswanatha Sarma A.  and Rambabu C., Indian J. Chem., 43A, 2518 (2004)
22. Nath G. Sahu and Paikaray, Indian J. Physics, 83 (4), 429 (2009) 429
23. Acharya S., Das B.K. and Mohanty G.C., Indian J. Phys. 83 (2), 185 (2009)
24. Subba Rao G., Ramajappa T. and  Kajagopal E., Indian J. Pure Appl. Phy., 26, 717 (1988)717
25. Anwar Ali, Anil Kumar Nain, Vinod Kumar Sharma and Shakil Ahmad, Indian J. Pure Appl.Phy.   42,666 (2004)

---

This work is licensed under a Creative Commons Attribution 4.0 International License.