Kinetics and Mechanism of Non-Isothermal Decomposition of Some Cross-Linked Metal-Alginate Complexes Especially Trivalent Metal -Alginate Complexes

Introduction

Alginic acid is a polysaccharide consisting of a binary heteropolymer structure of 1,4 linked β-D-mannuronic and α-L-guluronic acid units in a linear block copolymer structure.^1-3 It is well-known that alginate as anionic polyelectrolyte has a high affinity for crosslinking with polyvalent-

metal cations through formation  of partially coordinate and partially ionic bonds between those metal cations and the carboxylate and hydroxyl functional groups of alginate macromolecular chains, respectively, to metal-alginate complexes of an egg-carton like structur.^4,5

Although, most of these cross-linked metal alginate complexes in particularly the trivalent metal-alginates can be widely used in electronic devices [6-8] since possessed electrical properties lie in the range of semi- conductors, there is a few reports on the kinetics of their thermal decomposition [9-12]. Eventhough, the thermal decomposition of some trivalent metal alginates has been reported elsewhere [13]. Unfortunately, the kinetics and the mechanisms of their thermal decomposition still remain not complete.

In view of the foregoing aspects and our interesting in the thermal decomposition of macromolecules in particularly the polysaccharides [14-16], the present work has been undertaken with the aims at shedding highlights on the kinetics and mechanism of decomposition in terms of the kinetic models related to the construction and stability of the studied complexes.

Moreover, it aims to relate the composition, structure and material processing with the properties suitable for various technological applications such as semiconducting materials.^6-8

Experimental

Materials

All materials used were of Analar quality (BDH). The degree of substitution of sodium alginate used was found to be 4.34 mmol g^-1  (0.95 mol mol^-1). Doubly distilled conductivity water was used in all preparations. The measured viscosities using an Ubbelhode viscometer for a 4% alginate sol in water (w/w) were found to be 2.78 and 9.87 dl g^-1 for the inherent and reduced viscosities, respectively, at 25 °C.

Preparation of metal alginate complexes

Metal alginates in the form of granules were prepared by replacement of Na⁺ counter ions of alginate macromolecule by Al³⁺, Cr³⁺, Fe³⁺ ,Ce³⁺  and La³⁺ ions. This process was carried out by stepwise addition of the alginate powder reagent to electrolyte solutions of these metal ions (Ca. 0.5-1.0 M) whilst stirring the solutions vigorously in order to avoid the formation of lumps, which swell with difficulty. After completion of exchange processes, the metal-alginate granules formed were washed with deionized water several times, then, with doubly distilled water until the resulting washings became free from the non-chelated metal ions. The sample complexes were dried at about 105°C under vacuum over anhydrous CaCl₂ or P₂O₅.

FTIR spectra were recorded on a Pye unicam Sp 3100 spectrophotometer using the KBr disc technique (4000-200 cm^-1). The results are shown in Fig.1.

Figure 1: FTIR of Alginate, Ce(III)- and La(III) Alginate Complexes Click here to View figure

The data of elemental analysis of these metal-alginate complexes is summarized in Table 1.

Dynamic thermogravimetry of non-isothermal method was used to study the thermal decomposition of the present work rather than by conventional isothermal studies, owing to the advantages of the former one [9-13].  Thermogravimetry (TG) and differential thermogravimetry (DTG) analyses were carried out using a Mettler TA 3000 thermal analyzer in static air. Three heating rates 5, 10 and 20 K/min were used. A composite program was used for best fit the analysis.

Results

Stoichiometry

The exchange process is inherently a stoichiometric process [17]. Any , Na⁺ ,counter ions which leave the macromolecular chains of alginate must be compensated by an equivalent amount of the metal ions, even if the mobilities and valencies of the two exchangeable counter ions are quite different [18,19]. This is the necessary demands of electroneutrality.  Gravimetric analysis based on TGA data indicated that one mole of trivalent metal cation corresponds to three moles of alginate monomers in good agreement with either cited data of elemental analysis or that obtained from some  kinetic studies [20]. Then, the replacement of sodium counter ions, Na⁺, of alginate macromolecule by trivalent metal ion of the electrolyte solutions can be expressed by the following overall stoichiometric reactions

3 (Na – Alg)_n  + n M³⁺  = (M-Alg₃)_n +  (3 Na⁺ )_n                   (1)

Sol electrolyte gel electrolyte

where M denotes Al, Cr, Fe , Ce  or La metals.

The infrared spectra of the present complexes have been measured and the vibration assignments of the bands are cited in Table 2. It is well known that the bands correspond to the symmetry stretching vibrations of the –OCO^– (υ_s) in sodium alginate lie at 1400 cm^-1 and that of the asymmetric stretching vibrations (υ_as) lie at 1600 cm^-1, respectively [9-13,21]. Again, a broad band located near 3500 cm^-1 is owing to the stretching vibration of the hydrogen bond of water of the hydroxyl group. The free ligand has a strong band in the 1735 cm^-1. As shown in Fig. 1, the band of the stretching vibrations of  -OCO^– group is shifted from 1400 cm^-1(υ_s) to 1420-1425 cm^-1 whereas the band at 1600 cm^-1 (υ_as) is shifted to 1618-1698 cm^-1, respectively. This result indicates the participitation of  -OCO^– groups in the coordination. While, the shift in the υ_OH band to lower frequencies which became more broader than that of sodium alginate may also indicate the sharing of OH groups in the chelation processes.

The thermal decomposition curves of the studied complexes are shown in Fig. 2 compared to that reported for some other trivalent metal-alginate complexes [13] as shown in Fig. 3. However, the TG curves exhibit three stages of weight loss, the DTG curves indicate the presence of a series of thermal decomposition associated with the TG curves. This behavior is quite different from that of sodium alginate macromolecule [9, 10]. This difference may be interpreted by the difference in the strength of chelation in the formed partially ionic bonds between sodium and trivalent metal ions with carboxylate groups as well as to the formation of new partially coordinate bond between those trivalent metal ions and the hydroxyl groups in these complexes, whereas is absent in case of sodium alginate.

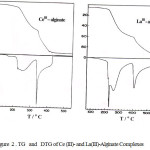Figure  2 : TG   and   DTG of Ce (III)- and La(III)-Alginate Complexes Click here to View figure

 

Figure 3: TGA and DTG of cross-linked Al (III)-, Cr(III)- and Fe(III)-   alginate complexes. Click here to View figure

The essential features of solid-state decomposition are the destruction of the crystal lattice of reactants, the breaking and redistribution of the chemical bonds and the formation of the crystal lattice of the decomposition products. In view of these aspects and great similarity between the experimental results to that observed for the thermal decomposition of Al-, Cr- and Fe-alginate complexes [13], a similar decomposition mechanism may be suggested.  This suggested mechanism indicates that the weight loss observed for the first stage in the TG curves (Table 3) can be explained by the evolution of four coordinated water molecules as follows,

3 (Na – Alg)_n  + n M³⁺  = (M-Alg₃)_n +  (3 Na⁺ )_n                   (1)

Sol                electrolyte          gel        electrolyte

where M denotes Al, Cr, Fe , Ce  or La metals.

The infrared spectra of the present complexes have been measured and the vibration assignments of the bands are cited in Table 2. It is well known that the bands correspond to the symmetry stretching vibrations of the –OCO^– (υ_s) in sodium alginate lie at 1400 cm^-1 and that of the asymmetric stretching vibrations (υ_as) lie at 1600 cm^-1, respectively [9-13,21]. Again, a broad band located near 3500 cm^-1 is owing to the stretching vibration of the hydrogen bond of water of the hydroxyl group. The free ligand has a strong band in the 1735 cm^-1. As shown in Fig. 1, the band of the stretching vibrations of  -OCO^– group is shifted from 1400 cm^-1(υ_s) to 1420-1425 cm^-1 whereas the band at 1600 cm^-1 (υ_as) is shifted to 1618-1698 cm^-1, respectively. This result indicates the participitation of  -OCO^– groups in the coordination. While, the shift in the υ_OH band to lower frequencies which became more broader than that of sodium alginate may also indicate the sharing of OH groups in the chelation processes.

The thermal decomposition curves of the studied complexes are shown in Fig. 2 compared to that reported for some other trivalent metal-alginate complexes [13] as shown in Fig. 3. However, the TG curves exhibit three stages of weight loss, the DTG curves indicate the presence of a series of thermal decomposition associated with the TG curves. This behavior is quite different from that of sodium alginate macromolecule [9, 10]. This difference may be interpreted by the difference in the strength of chelation in the formed partially ionic bonds between sodium and trivalent metal ions with carboxylate groups as well as to the formation of new partially coordinate bond between those trivalent metal ions and the hydroxyl groups in these complexes, whereas is absent in case of sodium alginate.

The essential features of solid-state decomposition are the destruction of the crystal lattice of reactants, the breaking and redistribution of the chemical bonds and the formation of the crystal lattice of the decomposition products. In view of these aspects and great similarity between the experimental results to that observed for the thermal decomposition of Al-, Cr- and Fe-alginate complexes [13], a similar decomposition mechanism may be suggested.  This suggested mechanism indicates that the weight loss observed for the first stage in the TG curves (Table 3) can be explained by the evolution of four coordinated water molecules as follows,

The weight losses associated with the second and third stages of the thermal decomposition (Table 3) may indicate the formation of transient fragments, followed by fast decomposition to give metal carbonate intermediates as in Eq. (3)

where M denotes cerium (III) or lanthanum (III) metal ions and C₁₈H₂₁O₁₇ corresponds to three combined monomers of alginate macromolecules chelated with the trivalent metal ions. This is followed by decomposition of the carbonate to give rise to metal oxides as final decomposition products as follows,

In case of Al-, Cr- and Fe-alginate complexes, the intermediate fragments were found to be hydroxide, oxalate and carbonate [13], respectively.

Discussion

Dealing with the non-isothermal kinetics for the TG curves, one can predict the kinetic mechanism by which the decomposition reaction takes place.

Hence, the application of thermoanalytical techniques for coordinated complexes such as is the present work is an example to study of the bonding and mechanism of decomposition, while the  thermogravimetry determines the kinetics. There are different methods for kinetic analysis of thermogravimetric data which can be carried out by the thermal and dynamic methods [22-31]. The kinetic model functions g(α) were examined here for each decomposition step using Sharp method [29]. In this method the isothermal reactions proceed in infinitesimal time intervals and, hence, the rates can be expressed by the Arrhenius type equation

where Z is the frequency factor, t is the time, α is the decomposition fraction and F(α) depends on the mechanism of the process.

Sharp and coworkers [31] suggested a reduced-time theoretical method, in order to distinguish between different methods where the time scale in the kinetic equation is

g(α) = kt                                                     (6)

where  g (α)  is the integrated form of F(α)  which altered so that

g(α)  =  A (t / t_0.5)                                              (7)

Here, t_0.5 is the time for 50% decomposition and A is a constant depending on the form of g(α).

The t_0.5 values corresponding to α = 0.5 were determined from the experimental data to curves of the form α (t / t_0.5) plots. The results data were analyzed by linear regression analysis for various kinetic model functions [27], The best fitting models for the decomposition steps for the investigated samples are summarized in Table 4.  It shows that both the phase boundary (R₃) and the random nucleation (A₃) give the best fit for the first dehydration decomposition steps with comparable correlation coefficients of first-order kinetics (F₁). The A₃ – function indicated that the nucleation of the thermal decomposition compound is a random process followed by a rapid surface growth. As nuclei grow larger they may eventually impinge on one another, so that growth ceases where they touch. On the other hand, R₃-function showed that the reaction is controlled by movement of interface at constant velocity and the phase decomposition is the phase-boundary controlled reaction. In general, the different kinetic mechanisms obtained may indicate that the nature of chelated metal ions and the geometrical model structures of the complexes control these kinetic parameters in decomposition of the given alginate complexes.

However, several methods can be used for calculation of the kinetic parameters from non-isothermal TG- data, Coasts-Redform [32] was generally used from the computation points of view. This method is the most convenient one and seems to be less tedious and has the advantages of leading for more accurate values of the kinetic parameters. According to this method, three heating rates 5, 10 and 20 K/min were employed using a small mass (~ 10 mg) to obtain reliable kinetic parameters. The activation energy (E_a) can be calculated from the following relationship

where Z denotes the frequency factor, Φ is the heating rate, T is the absolute temperature, T_c is the maximal temperature decomposition rate, (T_max) and R is the gas constant. For correct kinetic rate equation, plots of In g(α)/T² against 1/T should be linear as is observed experimentally. The activation energy (E_a) and frequency factor (Z) can be determined from the slopes and intercepts of such plots, respectively. These values for the first stage were calculated by using the method of least-squares and are summarized in Table 4.

Again the entropies of activations, ΔS*, were calculated from the following relationship

Z = (k_bT_max /h) exp^(ΔS*/R)                                      (9)

where k_b is the Boltzmann’s constant and h is the Plank’s constant [28]. The results of the first stage are summarized in Table 4. The negative values of entropy of activations at the initial dehydration step indicate that the reactants are more ordered than that of the activated complexes formed during the dehydration processes and vice versa for complexes of positive ΔS* values.

Moreover, the geometry of model structure of coordination may play a role in the stability of these metal alginate complexes. It is reported [33] that polyvalent metal ions chelate the functional groups, -COO^– and OH, of alginate macromolecule via either intra- or intermolecular association mechanisms depending on the nature, valency and coordination number of the chelated metal ions that allows a more stability of the complex formed. Divalent metal ions may use either inter- or intramolecular association mechanism through two carboxylate and one or more pairs of hydroxyl groups depending on the coordination number of the chelated metal ion (Scheme I). On the other hand, trivalent metal ions are restricted to only use the intermolecular association using three carboxylate groups and one or more pairs of the hydroxyl groups in chelation owing to geometrical reasons (Scheme II). This fact may be explained by the tendency of the trivalent metal ions to decrease the bond stretching resulting from elongation of metal-oxygen bonds in case of intramolecular association.

The magnitude of the activation energies and the maximal temperature decomposition degree rates may be considered as essential factors for determining the stability of these metal alginate complexes. The observed values reveal that the stability follows the following order(Ce – Alg₃)_n  > (La – Alg₃)_n   >  (Al– Alg₃)_n    >  (Cr – Alg₃)_n ≥ (Fe-Alg₃ )_n

This order agrees well with the magnitude of M-O bond energies in these metal–alginate complexes [34].

Table 1:  Elemental analysis for metal alginate complexes.

Complex	Found (%)			Calculated (%)			Formula	Reference
	C	H	M	C	H	M
AlIII-alginate	35.89	4.56	4.31	35.53	4.77	4.44	C18H21O17Al . 4 H2O	13
CrIII-alginate	34.33	4.55	8.24	34.12	4.58	8.21	C18H21O17Cr . 4 H2O	13
FeIII-alginate	33.82	4.41	8.88	33.92	4.55	8.74.	C18H21O17Fe . 4 H2O	13
CeIII-alginate	29.86	3.98	19.56	29.95	4.02	19.43	C18H21O17Ce . 4 H2O	This work
LaIII-alginate	29.75	4.00	19.67	30.00	4.03	19.30	C18H21O17La.4H2O

 

Table 2: Infrared frequencies (cm^-1) for sodium and metal alginate complexes.

Complex	υasOCO	υsOCO	υOH	υM—O	Reference
Na-alginate	1600	1400	3500	850	9
AlIII-alginate	1648	1425	3490	830	13
CrIII-alginate	1637	1420	3437	832	13
FeIII-alginate	1630	1422	3448	820	13
CeIII-alginate	1618	1421	3441	815	This work
LaIII-alginate	1698	1419	3426	842

 

Table 3: The maximum decomposition (T_max) and the weight loss accompanying the stages of decomposition (10 K) min.

 

Complex	Stage	TG			Weight loss  %	Tmax/ °C
		Ti/ °C	Tm/ °C	Tf/ °C
AlIII-alginate	1st	53	106	190	12.1	220
	2nd	190	220	340	52.7
	3rd	340	395	453	33.1
CrIII-alginate	1st	51	104	151	11.8	207
	2nd	151	207	342	25.9
	3rd	342	395	442	55.5
FeIII-alginate	1st	53	101	145	11.2	205
	2nd	145	205	289	38.2
	3rd	289	395	347	43.9
CeIII-alginate	1st	51	99	163	10.2	203
	2nd	163	203	267	39.5
	3rd	267	276	338	26.5
LaIII-alginate	1st	77	229	238	10.39	260
	2nd	238	260	385	34.67
	3rd	385	406	639	29.68

T_i : initial,  T_m : medium and T_f :  final

Table 4: Kinetic parameters for non-isothermal dehydration for cross- linked trivalent metal-alginate complexes.

 

 

Mteal-Alginate Complex	Heating Rate K min-1	Kinetic Model	E*a / kJmol-1	Log Z	ΔS* / JK-1 mol-1
		Stage
		1st	1st	1st	1st
AlIII –Alginate	5	F1	96	1.2×109	-75.3
	10	A3	88	6.1×108	-80.9
	20	A3	78	4.2×107	-103
CrIII –Alginate	5	F1	116	2.4×1010	-50.2
	10	F1	102	7.6 x109	-59.8
	20	F1	99	6.5 x109	-61.0
FeIII –Alginate	5	R3	201	1.2 x1014	20.7
	10	R3	214	3.1 x1012	8.96
	20	A3	120	1.6 x1010	-53.5
CeIII – Alginate	10	A3	198	–	–
LaIII – Alginate	10	A3	292	–	–

 

1. F. G. Fisher and H. Dorfel, Z. Physiol. Chem., 302 (1955) 186,
2. R. L. Whistler and K. W. Kirby. Z Physiol. Chem., 314 (1955) 46.
3. S. K. Chanda, E. L. Hirst, K. G. V. Percival and A. G. Koss, J. Chem.  Soc., (1952) 1833.
4. D. A. Rees, Biochem. J., 126 (1972) 257, F. R. Morris, D. A. Rees andT.Thomas, Carbohydr. Res., 66 (1967)  143.
5. I. Braccini, S. Perez, Biomacromol. , 2 (2001) 1089.
6. I. A. Zaafarany, K. S. Khairou and R. M. Hassan, High Perform. Polym22 (2009) 69.
7. K. S. Khairou and R. M. Hassan, High Perform. Polym., 14 (2002) 93.
8. R. M. Hassan, Coll. Surf., 60 (1991) 203.
9. A. A. Said and R. M. Hassan, Polym. Degrad. Slabil., 39 (1993) 393.
10. A. A. Said. M. M. Abd El-Wahab and R. M. Hassan, Thermochim. Acta,233 (1994) 13.
11. K. S. Khairou, J. Therm. Anal. Calor., 69 (2002) 583.
12. M. A. El-Gahami, K. S. Khairou and R. M. Hassan, Bull. Polish Acad.Sci., 61 (2003) 105.
13.  I. A. Zaafarany, JKAU Sci, Saudi Arabis, 22 (2010) 193.
14. F. A. A. Tirkistani, Carbohyd. Polym., 34 (1997) 329.
15. F. A. A. Tirkistani, Polym. Degrad. Stabil. , 60 (1998) 67.
16. F. A. A.  Tirkistani , Polym. Degrad. Stab. ,61 (1998) 161.
17. F. Helfferich, “Ion Exchange”, McGraw-Hill, New York, 1962, p. 250.
18. R. M. Hassan, A. Summan, M. K. Hassan, S. A. El-Shatoury, Eur.Polym. J., 25 (1989) 1209.
19. R. M. Hassan, M. Th. Mokhlouf, A. M. Summan and A. Awad, Eur.Polym. J., 25 (1989) 993.
20. F. A. A. Trkistani (forthcoming).
21. L. J. Bellamy, “The Infrared Spectra of Complex Molecules, 2nd Ed.,1966, p. 354.
22. A. W. Coats and J. P. Redferm, Analysis, 88 (1963) 906.
23. J. L. Sestak, Talanta, 13 (1966) 567.
24. E. S. Freeman and B. Carroll, J. Phys. Chem., 62 (1958) 394.
25. H. H. Horwitz and G. Metzger, Anal. Chem., 35 (1963) 1464.
26. J. Zsaks, J. Therm. Anal., 8 (1975) 593.
27. J. Zsaks and J. Zskako Jr., J. Therm. Anal., 19 (1980) 333.
28. J. L. Sestak and G. Berggen, Themochim. Acta, 3 (1971) 42.
29. T. Kojima, Therm. Anal. Calor., 64 (2001) 2.
30. S. Vicint, S. Margutti and E. Pedernonte, Therm. Anal. Calor., 66(2001) 343.
31. M. A. Moustafa, Z. A. Omaran, W. A. Bayoumy and M. A. Mousa,Therm. Anal. Calor., 63 (2001) 609.
32. J. P. Sharp, G. W. Brindley and B. N. N. Achar, Am. Chem. Soc., 49(1966) 379.
33. A. W. Coats and J. P. Redferm, Nature, 20 (1964) 68.
34. R. M. Hassan. Polym. Inter., 31 (1993) 81.
35. R. T. Sanderson, “Chemical   Bonds   and   Bond   Energy”, 2nd Ed., Academic Press, New York, 1976.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.