Understanding The Mechanism Of Stable Phosphorus Ylides Derived From Imidazole, 2-Methylimidazole Or 4-Methylimidazole: A Kinetic Study
M. Zakarianezhad1, S. M. Habibi-Khorassani2*, M. T. Maghsoodlou2 and B. Makiabadi3
1Department of Chemistry, Payame Noor University, Tehran, Iran. 2Department of Chemistry, University of Sistan and Baluchestan, Zahedan, Iran. 3Department of Chemical Engineering, Sirjan University of Technology, Sirjan, Iran.
Kinetic studies have been made for synthesis of stable phosphorus ylids in the presence of different NH-acids, such as Imidazole, 2-Methylimidazole or 4-Methylimidazole (as a protic/nucleophilic reagent). At different temperature range studied, the dependence of the second order rate constant (ln k2) and (ln k2/T) on reciprocal temperature was in a good agreement with Arrhenius and Eyring equations. This provided the relevant plots to calculate the activation parameters (Ea, ?H*, ?S* and ?G*) of all reactions. Furthermore, useful information were obtained from studies of the effect of solvent, structure of reactants (dialkyl acetylenedicarboxylates) and also concentration of reactants on the reaction rates. Proposed mechanism was confirmed according to the obtained results and steady state approximation, first and third steps (k2 and k3) of all reactions was recognized as a rate determining and fast steps, respectively on the basis of experimental data.
KEYWORDS:Stable phosphorus ylides; Dialkyl acetylenedicarboxylates; NH-acid; heterocyclic compounds; Kinetic studies
Download this article as:| Copy the following to cite this article: Zakarianezhad M, Habibi-Khorassani S. M, Maghsoodlou M. T, Makiabadi B. Vanadatesulfuric Acid-Catalyzed Novel And Eco-Benign One-Pot Synthesis Of Polyhydroquinoline Derivatives Under Solvent-Free Conditions. Orient J Chem 2012;28(3). |
| Copy the following to cite this URL: Zakarianezhad M, Habibi-Khorassani S. M, Maghsoodlou M. T, Makiabadi B. Vanadatesulfuric Acid-Catalyzed Novel And Eco-Benign One-Pot Synthesis Of Polyhydroquinoline Derivatives Under Solvent-Free Conditions. Available from: http://www.orientjchem.org/?p=22959 |
Introduction
Organophosphorus compounds have emerged as important reagents and intermediates in organic synthesis [1].An important group of this class is phosphorus ylides, which have been used in many reactions and synthesis of organic compounds [2-29].The prominent role of these compounds is to convert the carbonyl groups to carbon-carbon double bonds [7] from the large number of methods available for the synthesis of phosphorus ylides, the most important involve the reaction of a phosphonium salt with a base [14, 20]. In recent years a method has been developed for the preparation of this family by using a novel approach employing vinyl phosphonium salts [15, 16]. The phosphonium salts are most often converted to the ylides by treatment with a strong base, though weaker bases can be used if the salt is acidic enough. Michael addition of phosphorus (ш) compounds such as triphenylphosphine to acetylenic esters leads to reactive 1, 3-dipolar intermediate betaines which are not detected even at low temperature [17]. These unstable species can be trapped by a protic reagent, ZH, such as methanol, amide, imide, etc. to produce various compounds e.g. ylides [5-29]. A facile synthesis of the reaction between triphenylphosphine 1, dialkyl acetylenedicarboxilates 2 (2d, 2e or 2f) and Imidazole, 2-Methylimidazole or 4-Methylimidazole 3 (3a, 3b or 3c) (as NH-acid) has been reported earlier [30] but the kinetic studies of this reaction has not been investigated yet. In order to gain further insight into the reaction mechanism, a kinetic study of the reaction between compounds 1, 2 and 3 as NH-acid was undertaken by the UV spectrophotometer technique. On the basis of the well established chemistry of trivalent phosphorus nucleophiles, [1-3]it is reasonable to assume that phosphorus ylide 4 results from the initial addition of triphenylphosphine to the acetylenic ester 2 (2d, 2e or 2f) (rate constant k2) and subsequent protonation of the 1:1 adduct by the NH-acid 3 (3a, 3b or 3c) (rate constant k3) to form phosphoranes 4 (rate constant k4). To gain further insight into the reaction mechanism between triphenylphosphin 1, dialkyl acetylenedicarboxylates 2 and 3 (3a, 3b or 3c) (as NH- heterocyclic compound) for generation of phosphorus ylids 4 (Figure 1), a kinetic study of the reactions was undertaken by UV spectrophotometeric technique.
Experimental
Chemicals and Apparatus Used
Dialkyl acetylenedicarboxylates, triphenylphosphine and Imidazole, 2-Methylimidazole and 4-Methylimidazole were purchased from Fluka (Buchs, Switzerland) and used without further purifications. All extra pure solvents including the 1,4-dioxan and 1,2-dichloroethane also obtained from Merck (Darmstadt, Germany). A Cary UV/Vis spectrophotometer model Bio-300 with a 10 mm light-path quartz spectrophotometer cell was employed throughout the current work.
Method
To find the appropriate wavelength to follow the kinetic study of the reaction, in the first experiment, 3×10-3 M solution of triphenylphosphine 1, di-tert-butyl acetylenedicarboxylate 2f and Imidazole 3a was prepared in 1,4-dioxan as solvent. The relevant spectra of each compound were recorded over the wavelength range 190-400 nm. Figures 2, 3 and 4 show the ultraviolet spectra of compounds 1, 2f and 3a respectively. In a second experiment, a 1mL aliquot from the 3×10-3 M solutions of each compound of 1 and 3a was pipetted first into a quartz spectrophotometer cell (as there is no reaction between them), later 1mL aliquot of the 3×10-3M solution of reactant 2f was added to the mixture and the reaction monitored by recording scans of the entire spectra every 8 min over the whole reaction time at ambient temperature. The ultra-violet spectra shown in Figure 5 are typical. From this, the appropriate wavelength was found to be 330 nm (corresponding mainly to triphenylphosphine 1). Since at this wavelength, compounds 1, 2f and 3a have relatively no absorbance value, so provided the
Figure 1: The reaction between triphenyl phosphine 1, dialkyl acatylenedicarboxylate 2 (2d, 2e or 2f) and 3 (3a, 3b or 3c) for generation of stable phosphorus ylids 4.
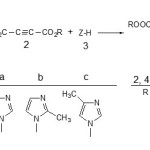 |
Figure 1:The reaction between triphenyl phosphine 1, dialkyl acatylenedicarboxylate 2 (2d, 2e or 2f) and 3 (3a, 3b or 3c) for generation of stable phosphorus ylids 4
|
opportunity to fully investigate the kinetics of the reaction between triphenylphosphine 1, di-tert-butyl acetylenedicarboxylate 2f and imidazole 3a. The UV-vis spectra of compound 4af were measured over the concentration range (2×10-4M ≤ M4c ≤10-3M) to check for a linear relationship between absorbance values and concentrations. With the suitable concentration range and wavelength identified, the following procedure was employed.
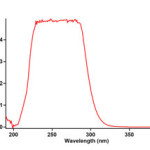 |
Figure 2:The UV spectrum of 10-3M triphenyphosphine 1 in 1,4-dioxan
|
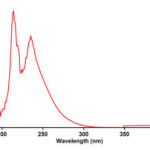 |
Figure 3: The UV spectrum of 10-3M di-tert-butyl acetylenedicarboxylate 2f in 1,4-dioxan.
|
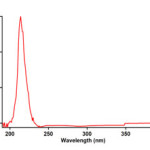 |
Figure 4:The UV spectrum of 10-3M imidazole 3a in 1,4-dioxan
|
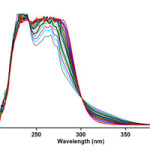 |
Figure 5:UV spectra of the reaction between 1, 2f and 3a with 10-3M concentration of each compound as reaction proceeds in 1,4-dioxan
|
Figure 5. The UV spectra of the reaction between 1, 2f and 3a with 10-3M concentration of each compound as reaction proceeds in 1,4-dioxan.
The reaction kinetics was followed by plotting UV absorbance against time 12.0ºC. Figure 6 shows the absorbance change (dotted line) versus time for the 1:1:1 addition reaction between compounds 1, 2f and 3a at 12.0ºC. The infinity absorbance (A∞) that is the absorbance at reaction completion, can be obtained from Figure 6 at t =152 min. With respect to this value, zero, first or second curve fitting could be drawn automatically for the reaction by the software [31] associated with the UV instrument. Using the original experimental absorbance versus time data provided a second-order fit curve (solid line) that fits exactly the experimental curve (dotted line) as shown in Figure 7. Thus, the reaction between triphenylphosphine 1, di-tert-butyl acetylenedicarboxylate 2f and imidazole 3a follows second-order kinetics. The second-order rate constant (k2) is then automatically calculated using a standard equation within the program at 12.0ºC is reported in Table 1. Furthermore, kinetic studies were carried out using the same concentration of each reactant in the continuation of experiments with concentrations of 5×10-3 M and 7×10-3 M respectively. As expected, the second-order rate constant was independent of concentration and its value was the same as in the previous experiment. In addition, the overall order of reaction was also 2.
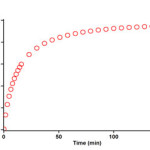 |
Figure 6: Experimental absorbance change (dotted line) against time at 330 nm for the reaction between compounds 1, 2f and 3a at 12.0ºC in 1,4-dioxan.
|
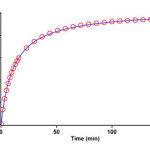 |
Figure 7: Second order fit curve (solid line) accompanied by the original experimental curve (dotted line) for the reaction between 1, 2f and 3a at 330 nm and 12.0ºC in 1,4-dioxan.
|
Table 1 The values of second order rate constant for the three reactions (1, 2f and 3a), (1, 2f and 3b) and (1, 2f and 3c) in the presence of different solvents at all temperatures investigated.
|
Reaction
|
Solvent
|
k2.M-1.min-1 |
|||
|
12.0ºC |
17.0ºC |
22.0ºC |
27.0ºC |
||
|
1, 2f and 3a |
1,4-dioxan |
58.8 |
74.7 |
88.9 |
111.4 |
|
Mix (50/50%) |
71.6 |
89.8 |
107.4 |
136.4 |
|
|
ethyl acetate |
92.7 |
113.9 |
139.3 |
162.4 |
|
|
1, 2f and 3a |
1,4-dioxan |
51.4 |
59.9 |
72.8 |
87.8 |
|
Mix (50/50%) |
66.1 |
81.7 |
91.7 |
122.8 |
|
|
ethyl acetate |
71.8 |
87.9 |
110.9 |
138.3 |
|
|
1, 2f and 3a
|
1,4-dioxan |
53.8 |
67.3 |
84.1 |
93.0 |
|
Mix (50/50%) |
69.2 |
85.5 |
100.3 |
128.1 |
|
|
ethyl acetate |
80.9 |
98.9 |
125.3 |
148.6 |
|
Results and Discussion
Effect of Solvent and Temperature
To determine the effect of change in temperature and solvent environment on the rate of reaction, it was elected to perform various experiments at different temperatures and solvent polarities but otherwise under the same conditions as for the previous experiment. For this purpose, 1,2-dichloroethane and mixture of 1,4-dioxan and 1,2-dichloroethane (50/50% (V/V)) with 10.3 and (2 < ε < 10.3) dielectric constant respectively were chosen as a suitable solvent since it is not only could be dissolved all compounds but also did not react with them. The results show that the rate of reaction in each case was increased at higher temperatures. In addition, the rate of reaction between 1, 2f and 3a was accelerated in a higher dielectric constant environment (1,2-dichloroethane) in comparison with a lower dielectric constant environment (1,4-dioxan) at all temperatures investigated. In the temperature range studied, the dependence of the second-order rate constant (ln k2) of the reactions on reciprocal temperature is consistent with the Arrhenius equation, giving activation energy of reaction from the slope of Figure 8.
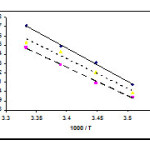 |
Figure 8: Dependence of second order rate constant (ln k2) on reciprocal temperature for the reaction between compounds 1, 2f and 3a (solid line), 1, 2f and 3b (dash line) and 1, 2f and 3c (dotted line) measured at wavelength 330 nm in 1,4-dioxan in accordance with Arrhenius equation.
|
Effect of Concentration
To determine reaction order with respect to triphenylphosphine 1 and dialkyl acetylenedicarboxylate 2 (2f), in the continuation of experiments, all kinetic studies were carried out in the presence of excess 3a. Under this condition, the rate equation may therefore be expressed as:
In this case (3×10-2 M of 3a instead of 3×10-3 M) using the original experimental absorbance versus time data provides a second order fit curve (full line) against time at 330 nm which exactly fits the experimental curve. The value of rate constant was the same as that of obtained from the previous experiment (3×10-3 M). Repetition of the experiments with 5×10-2M and 7×10-2M of 3a gave, separately, the same fit curve and rate constant. In fact, the experimental data indicated that the observed pseudo second order rate constant (kobs) was equal to the second order rate constant (k2), this is possible when γ is zero in equation (1). It is appears, therefore, that the reaction is zero and second order with respect to 3a (protic/nucleophilic reagent) and the sum of 1 and 2 (2f) (α + β = 2), respectively.
To determine reaction order with respect to dialkyl acetylenedicarboxylate 2 (2f), the continuation of experiment was performed in the presence of excess of 1 (rate = k΄obs [3]γ [2]β, k΄obs = k2 [1]α(2)). The original experimental absorbance versus time data and provide a pseudo first order fit curve at 330 nm, which exactly fits the experimental curve (dotted line) as shown in Figure 9.
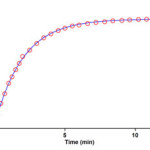 |
Figure 9. Pseudo first order fit curve (solid line) for the reaction between 2f and 3a in the presence of excess 1 (10-2 M) at 330 nm and 12.0˚C in 1,4-dioxan
|
As a result since γ = 0 (as determined previously), it is reasonable to accept that the reaction is first order with respect to compound 2 (2f) (β =1). Because the overall order of reaction is 2 (α + β + γ =2) it is obvious that α = 1 and order of triphenylphosphine 1 must be equal to one. This observation was obtained also for reactions between (1, 2e and 3a) and (1, 2d and 3a). Based on the above results, a simplified proposed reaction mechanism is shown in Figure 10.
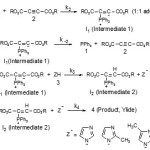 |
Figure 10. Mechanism proposed for the reaction between 1, 2 (2d, 2e or 2f) and 3 (3a, 3b or 3c) on the basis of literatures for generation of phosphorus ylides 4.
|
The experimental results indicate that the third step (rate constant k3) is possibly fast. In contrast, it may be assumed that the third step is the rate determining step for the proposed mechanism. In this case the rate law can be expressed as follows:
The steady state assumption can be employed for [I1] which is generated following equation,
The value of [I1] can be replaced in equation (3) to obtain this equation:
Since it was assumed that k3 is relevant to the rate determining step, it is reasonable to make the following assumption: k-2 >> k3 [3]
So the rate of low becomes:
The final equation is indicates that overall order of reaction is three which is not compatible with experimental overall order of reaction (=two). In addition, according to this equation, the order of reaction with respect to maleimide 3 is one, whereas it was actually shown to be equal to zero. For this reason, it appeared that the third step is fast. If we assume that the fourth step (rate constant k4) is the rate-determining step for the proposed mechanism, in this case, there are two ionic species to consider in the rate determining step, namely phosphonium ion (I2) and maleimide ion (Z–). The phosphonium and maleimide ions, as we see in Figure 10, have full positive and negative charges and form very powerful ion-dipole bonds to the 1,2-dichloroethane, the high dielectric constant solvent. However, the transition state for the reaction between two ions carries a dispersed charge, which here is divided between the attacking maleimide and the phosphonium ions. Bonding of solvent (1,2-dichloroethane) to this dispersed charge would be much weaker than to the concentrated charge of maleimide and phosphonium ions. The solvent thus stabilize the species ions more than it would the transition state, and therefore Ea would be higher, slowing down the reaction. However, in practice, 1,2-dichloroethane speeds up the reaction and for this reason, the fourth step, which is independent of the change in the solvent medium, could not be the rate determining step. Furthermore, the rate law of formation of the product (fourth step) for a proposed reaction mechanism with application of steady state assumption can be expressed by: rate =k4 [I2] [Z–]
By application of steady state for [I2] and [Z–], and replacement of their values in the above equation, the following equation is obtained:
This equation is independent of rate constant for the fourth step (k4) and shows why the fourth step would not be affected by a change in the solvent medium. In addition, it has been suggested earlier that the kinetics of ionic species‘ phenomena (e.g. the fourth step) are very fast [32-34]. If the first step (rate constant k2) were the rate determining step, in this case, two reactants (triphenylphosphine 1 and dialkyl acetylenedicarboxylate 2), as we see in Figure 10, have no charge and could not form strong ion-dipole bonds to the high dielectric constant solvent, 1,2-dichloroethane. However, the transition state carries a dispersed charge which here is divided between the attacking 1 and 2 and, hence, bonding of solvent to this dispersed charge is much stronger than the reactants, which lack charge. The solvent thus stabilizes the transition state more than it does the reactants and, therefore, Ea is reduced which speeds up the reaction. Our experimental results show that the solvent with higher dielectric constant exerts a power full effect on the rate of reaction (in fact, the first step has rate constant k2 in the proposed mechanism) but the opposite occurs with the solvent of lower dielectric constant, (see Table 1,). The results of the current work (effects of solvent and concentration of compounds) have provided useful evidence for steps 1 (k2), 3 (k3) and 4 (k4) of the reactions between triphenylphosphine 1, dialkyl acetylenedicarboxylate 2 (2a, 2b or 2f) and 3 (3a, 3b or 3c). Two steps involving 3 and 4 are not determining, although the discussed effects, taken altogether, are compatible with first step (k2) of the proposed mechanism and would allow it to be the rate-determining step. However, a good kinetic description of the experimental result using a mechanistic scheme based upon the steady state approximation is frequently taken as evidence of its validity. By application of this, the rate formation of product 4 from the reaction mechanism (Figure 10) is given by:
We can apply the steady-state approximation to [I1] and [I2];
To obtain a suitable expression for [I2] to put into equation (5) we can assume that, after an initial brief period, the concentration of [I1] and [I2] achieve a steady state with their rates of formation and rates of disappearance just balanced. Therefore and are zero and we can obtain expressions for [I2] and [I1] as follows:
We can now replace [I1] in the equation (6) to obtain this equation:
The value of [I2] can be put into equation (5) to obtain the rate equation (8) for proposed mechanism: or
Since experimental data were indicated that steps 3 (k3) and 4 (k4) are fast but step 1 (k2) is slow, it is therefore reasonable to make the following assumption:
So the rate equation becomes:
This equation which was obtained from a mechanistic scheme (shown in Figure 10) by applying the steady-state approximation is compatible with the results obtained by UV spectrophotometery.
Further Kinetic Investigations
Effect of Structure of Dialkyl acetylenedicarboxylates
To confirm the above observations, further experiments were performed with diethyl acetylenedicarboxylate 2e and dimethyl acetylenedicarboxylate 2d, respectively, under the same conditions used in the previous experiments. The values of the second-order rate constant (k2) for the reactions between (1, 2e and 3) and (1, 2d and 3) are reported in Tables 2 and 3, for all solvents and temperatures investigated.
As can be seen from Tables 2 and 3 the behavior of diethyl acetylenedicarboxylate 2e and dimethyl acetylenedicarboxylate 2d is the same as for the di-tert-butyl acetylenedicarboxylate 2f with respect to the reaction with triphenylphosphine 1 and NH-acid 3 (3a, 3b and 3c). The rate of the former reactions was also accelerated in a higher dielectric constant environment and with higher temperatures; however, these rates under the same condition are approximately 9 to 11 times more than for the reaction with di-tert-butyl acetylenedicarboxylate 2f. It seems that both inductive and steric factors for the bulky alkyl groups in 2f tend to reduce the overall reaction rate (see equation 9). In the case of dimetyl acetylenedicarboxylate 2d, the lower steric and inductive effects of the dimethyl groups exert a powerful effect on the rate of reaction. With respect to the equation (9) that is overall reaction rate, the activation parameters involving DG#, DS# and DH# could be now calculated for the first step (rate determining step), as an elementary reaction, on the basis of Eyring equation. The results are reported in Table 4.
Table 4: The activation parameters involving DG#, DS# and DH#for the reactions between (1, 2f and 3), (1, 2b and 3) and (1, 2a and 3) in 1,4-dioxan
|
Reaction |
DG#(kJ.mol-1) |
DH#(kJ.mol-1) |
DS#(J.mol-1.K-1) |
|
1, 2f and 3a |
70.9 |
27.3 |
-148.9 |
|
1, 2e and 3a |
65.9 |
16.2 |
-170.1 |
|
1, 2d and 3a |
65.0 |
11.0 |
-184.5 |
Effect of structure of NH-acids
Reproducible experiments were investigated in the presence of other NH-acids such as 4-methyl imidazole 3c or 2-methyl imidazole 3b under the same conditions used in the previous experiments, the rate of reactions were reduced in comparison with imidazole 3a respectively. It seems that the effect of electron donor of substituted methyl group in positions 2 and 4 of imidazole ring would tend to reduce the chemical activity of NH-acids in these compounds. This effect in 2-methylimidazole is more than 4-methylimidazole. Practically, experimental data were indicate that change within the structure of NH-acid has no effect on the priority of the rate determining step of the reaction and step 1 (rate constant k2) is still the rate determining step, in the presence of new NH-acids 3c or 3b and order of reaction with respect to them is still zero. Because of the chemical activity of NH-acid is dependent on its structure, this provide opportunity in order to change the rate constant k3 (NH-acid participate in this step) and also subsequent alteration of overall rate constant of reaction (see equation 8).
Conclusion
Kinetic investigation of recent reactions was undertaken using UV spectrophotometry. The results can be summarized as follow: (1) the appropriate wavelengths and concentrations were determined to follow the reaction kinetics. (2) The overall reaction order followed second-order kinetics and the reaction orders with respect to triphenylphosphine 1, dialkyl acetylenedicarboxylate 2 and NH-acid 3 were one, one and zero respectively. (3) The values of the second-order rate constants of all reactions were calculated successfully at all solvents and tempratures investigated (4) The rates of all reactions were accelerated at higher temperatures. Under the same conditions, the activation energy for the reaction with di-tert-butyl acetylenedicarboxylate 2f (29.7 kJ/mol) was higher than that for the both reactions which were followed by the diethyl acetylenedicarboxylate 2e (18.6 kJ/mol) and dimethyl acetylenedicarboxylate 2d (13.4 kJ/mol) in 1,4-dioxan (5) The rates of all reactions were increased in solvents of higher dielectric constant and this can be related to differences in stabilization by the solvent of the reactants and the activated complex in the transition state. (6) Increased steric bulk in the alkyl groups of the dialkyl acetylenedicarboxylates, accompanied by the correspondingly greater inductive effect, reduced the overall reaction rate. (7) With respect to the experimental data, the first step of proposed mechanism was recognized as a rate-determining step (k2) and this was confirmed based upon the steady-state approximation. (8) Also, the third step was identified as a fast step (k3). (9) The activation parameters involving DG#, DS# and DH# were reported for three reactions.
Acknowledgments
Authors sincerely thank the Universities of Sistan & Baluchestan and payame noor for providing financial support of this work.
References
- Crayson M. and Griffith E.J., Topics in Phosphorus Chemistry, vol. 7, Insterscience, New York, (1972).
- Hudson H.R., Primary, Secondary and Tertiary Phosphines, Plyphosphines and Heterocyclic Organophosphorus (ш) Compounds, in the Chemistry of Organophosphorus Compounds, Wiley: New York, (1990).
- Engel R., Synthesis of Carbon-phosphorus Bonds, CRC Press, Boca Rotan, FL, (1988).
- Cadogan J.I.G., Organophosphorus Reagent in Organic Synthesi, Academic press, New York, (1979).
- Ramazani A. Noshiranzadeh N. Ghamkhari A. Slepokura K. and Lis T., Helv. Chim. Acta., 91, 2252(2008).
- Ramazani A Kazemizadeh A. R. Ahmadi E. Noshiranzadeh N. and Souldozi A., Current Organic Chemistry., 12, 59(2001).
- Maryanoff B. E. and Reitz A. B., Chem. Rev., 89, 863(1989).
- Maghsoodlou M. T. Hazeri N. Habibi-Khorassani S. M. Moeeni Z. Marandi Gh. Lashkari M. Ghasemzadeh M. and Bijanzadeh H. R., J. Chem. Res., 566(2007).
- Anary-Abbasinejad M. Anaraki-Ardakani H. and Hosseini-Mehdiabad H., Phosphorus Sulfur and Silicon Relat. Elem., 183, 1440(2008).
- Hassanabadi A. Anary-Abbasinejad M. and Dehghan A., Synth. Commun., 39132(2009).
- Anaraki-Ardakani H. Sadeghian S. Rastegari F. Hassanabadi A. Anary-and Abbasinejad M., Synth. Commun., 38, 1990(2008)
- Yavari I. Adib M. Jahani-Mogaddam F. and Sayahi M. H., Phosphorus Sulfur and Silicon Relat. Elem., 177, 545(2002).
- Kazemian M. A. Nassiri M. Ebrahimi A. Maghsoodlou M. T. Habibi-and Khorassani S. M., Arkivoc., xvii, 173(2008).
- Fitjer, L. and Quabeck U., Synth. Commun., 15, 855(1985).
- Ramazani A. and Souldozi A., Phosphorus Sulfur Silicon Relat. Elem., 180, 2801(2008).
- Yavari I. and Alizadeh A. A., Monatsh. Chem., 134, 435(2003).
- Ramazani A. and Bodaghi A., Tetrahedron Lett., 41, 567(2000).
- Wang Z. G. Zhang G. T. Guzei I. and Verkade J. G., J. Org. Chem., 66, 3521(2001).
- Islam M. R. Hassan Z. and Saidi K., Synth. Commun., 33, 65(2003).
- Keglevich G. Baan Z. and Hermecz I., Current Organic Chemistry., vol. 11, 107(2007).
- Yavari I. and Ahmadian-Rezligh L., Phosphorus Sulfur and Silicon Relat. Elem., 181, 771(2006).
- Adib M. Mostof M. Ghanbary K. and Bijanzadeh H. R., Synthesis., 10, 1663(2005).
- Kalantari M. Islami M. R. Hassani Z. and Saidi K., Arkivoc., x, 55(2006).
- Islam M. R. Mollazeh F Badiei A and Sheibani H., Arkivoc., xv, 25(2005).
- Maghsoodlou, M. T. Habibi-Khorassani S. M. Rofouei M. K. Adhamdoust S. R. Nassiri M., Arkivoc., xii, 145(2006).
- Maghsoodlo M. T. Hazeri N. Habibi-Khorassan S. M. Ghulame-Shahzadeh A. and Nassiri M., Phosphorus Sulfur and Silicon Relat. Elem., 181, 913(2006).
- Habibi-Khorassan S. M. Maghsoodlou M. T. Ebrahimi A. Zakarianejad M. and Fattahi M., J. Solution Chem., 36, 1117(2007).
- Sasaki S. and Yoshifuji M., Current Organic Chemistry., 11, 17(2001).
- Habibi-Khorassani S. M. Maghsoodlou M. T. Nassiri M. Zakarianejad M. and Fattahi M., Arkivoc., xvi, 168(2006).
- Maghsoodlou M. T. Habibi-khorassani S. M. Hazeri N. Nassiri M. and Kakaei, R., Phosphorus, Sulfur and Silicon., 181, 553(2006).
- Schwartz L. M. and Gelb R. I., Anal. Chem., 50, 1592(1978).
- Okubo T. Maeda, Y. and Kitano, H., J. Phys. Chem., 93, 3721(1989).

This work is licensed under a Creative Commons Attribution 4.0 International License.









