Temperature Dependent Equation of State for Solids

Introduction

It is of great importance in geosciences to explain the thermo elastic behavior of minerals, ionic and metallic solids, alloys etcpresent in deep interior of the earth under high pressure and high temperature conditions. It helps indisclosing the secretfacts about the evolution and dynamics of the earth. The structure, stability, atomic and molecular interactions in the material due to different pressure and temperatures modifies the physical properties of the solid materials.Also the physical properties of solids are greatlyinfluencedby its sizes and shapesandinturnseffect the geo physical processes [1, 2, 3].

Thermodynamical study of solids under varying temperature and pressure conditions has widespread applications in physics, engineering and material sciences and predicts the mechanical aspects of solid materials under high pressure and high temperature. The equation of state (EOS) is a thermodynamical relation which explains the dependence of one variable on other variables [4, 5]. An equation of state can be applied successfully to explain the behavior of solids undervarying pressure and temperature and helps to obtain the extrapolated values in the regions where the experimental data are not available [6, 7].Several theoretical and experimental studies have been performed during past[8-16] to explain the behavior of solidsunder varying temperature pressure conditions. However, there is always a scope for the better approach which may be more efficient and applicable to predict the better results and therefore amore efficient equation of state is required to explain the temperature and pressure dependent anharmonic behavior of solids under extreme temperature and pressure conditions.  With this objective, we have formulated a pressure-volume-temperature dependent thermodynamic equation of state in the present study. The equation of stateso developedis employed for the analysis of thermoelastic properties ofNaCl, as an exampleto verify its applicability. The reason for considering the NaCl crystal as an example because of the fact that it has simple structure and remains stable up to the pressure of about 30 GPa and has a very high melting temperature of 1074 K.It is, therefore, widely used as a pressure and temperaturecalibrant [17, 18]. Moreover, the experimental data are easily available for NaCl and therefore, the calculated results could be compared to check the validity and applicability of the present theoretical approach.The methodology is described in section 2 and the results obtained are discussed in section 3.

Method of Analysis

The Suzuki EOS based on Gruneisen theory of thermal expansivity [19, 20] reads as follows

Excluding the thermal effect, the equation in terms of Pressure P is expressed as:

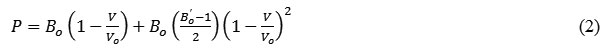
The expressions for the bulk modulus (B) and its first order pressure derivative (B’) obtained from Suzuki EOS (eq. 2) can be written as

which gives  B’ = B’_O – 2 on applying the thermodynamic boundary condition at P=0;  V = V_O, instead of B’ = B’_O, therefore,Suzuki EOS (eq. 2) is not mathematically and thermodynamically consistent.

The modified form of pressure dependent  Suzuki equation of state formulated by Goyal and Gupta [21] is obtained by considering the pressure variation with respect to change in volume (^ΔV/V) up to quadratic term as follows

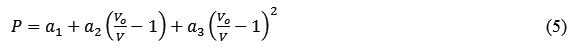
where a₁, a₂ and a₃ are the constant parameters. V_o is initial volume at P = 0 and V/V_o is the volume compression.

The expression of bulk modulus B = -V(dp/dv) is obtained on differentiating equation (5) w.r.t. volume as follows

Applying the initial boundary conditions in equation (5) and equation (6), i.e. B = B_o, V=V_o at P = 0; the constants a₁, a₂ and a₃ are calculated as follows

Substituting the values of a₁, a₂ and a₃ from eq. (7) in equation (5), the pressure dependent equation of state formulated by Goyal and Gupta EOS [21] is of form:

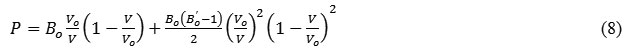
The expression for bulk modulus so obtained using equation (7) in equation (6) is as follows

And its first order pressure derivative is obtained as follows

which gives B’ = B’_O on applying the thermodynamic boundary condition at P=0; V=V_o , therefore, equation (8) is thus mathematically and thermodynamically consistent.

The inverted form of isothermal equation (8) in terms of volume compression is expressed likewise

Equation (11) is isothermal equation of state in terms of volume compression.

To make the eq. (11) as temperature dependent equation of state,the pressure applied on the solid must be expressed as under [4]:

where P_Th  is the internal thermal pressure arises due to the application of external pressure on solid [22].

Substituting P from eq. (12) to include thethermal Effect in equation (11),we get

where α_O is coefficient of thermal expansion; T_O  is room temperature and T is some elevated temperature.

Using equation(14) in equation (13) at P=0, the isobaric form of new equation can now be expressed as follows

Considering v_o/v = X , obtained in equation (15); the expression for bulk modulus in terms of change in volume is found as follows

It is assumed that the product of volume thermal expansion coefficient (α_T) and the bulk modulus (B_T) is constant at constant temperature [23], i.e.

and therefore, the volume thermal expansion coefficient is expressed as follows

The new equation of state at variable pressures-temperatures is thus obtained as follows

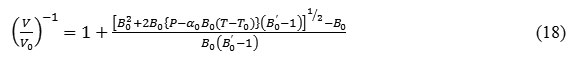
Results and Discussions

To test the validity and applicability of the present equation of state, the volume expansion is studied in NaCl crystal over the temperature range 298K- 773K under zero pressure conditions using isobaric equation (15). The input data needed for the calculation at room temperature and zero pressure are taken as:

The calculated values of thermal expansion(V/V₀)obtained by using the isobaric EOS (equation 15) at different temperatures are compared with the experimental data and shown in figure 1. It is clear from the figure 1 that the results found in the present study are in good agreement with the available experimental dataand encouraged to calculate the values of thermal expansion coefficient and bulk modulus under high temperature too.

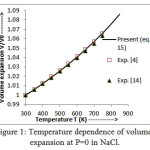Figure 1: Temperature dependence of volume expansion at P=0 in NaCl.   Click here to View table

 

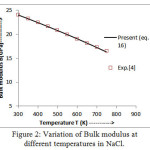Figure 2: Variation of Bulk modulus at different temperatures in NaCl.   Click here to View table

 

The values of bulk modulus and thermal expansion coefficient (TEC) calculated from modified equation (16) and equation (17) are shown in figures 2 and 3 respectively.The results so obtained are compared with the experimental values [4, 14] which present a very close agreement. It is noted from figure 2 that the trend of variation of bulk modulus is in decreasing order with increasing temperature which is a normal trend in solids.However, thermal expansion coefficient (TEC) increases with temperature as shown in figure 3.

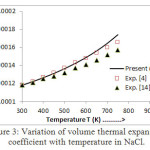Figure 3: Variation of volume thermal expansion coefficient withtemperature in NaCl.   Click here to View table

 

The present model theory is further applied to analyze the volume compression in NaClover the pressure range from 0 to 30 GPa at different isotherms. The values calculated by using the equation (18) are shown in figures 4-9 along with the experimental data. It can be noted from figures 4-9 that our results are in close agreement with the available experimental data.

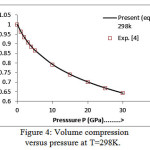Figure 4: Volume compression versus pressure at T=298K.   Click here to View table

 

It is pertinent to mention here that the results achieved in the present study from the modified Suzuki equation of state as derived by Goyal and Gupta [21] is mathematically and thermodynamically consistent and predicts values at high temperatures, successfully. However, original Suzuki equation of state [19, 20] yields imaginary values at high temperatures and is not capable of explaining the thermal expansion coefficient at T>736 K at P=0 [4].The calculated values of thermal expansion coefficient and bulk modulus of NaCl crystal thus justify the quasi -harmonic approximation. On the basis of overall analysis and a close agreement of our theoretical results with the experimental values validates the present theoretical approach which may be useful for the researcher workingwithhigh temperature and high pressure studies.

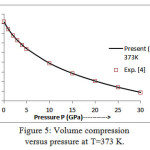Figure 5: Volume compression versus pressure at T=373 K.   Click here to View table

 

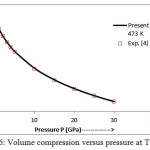Figure 6: Volume compression versus pressure at T=473 K.   Click here to View table

 

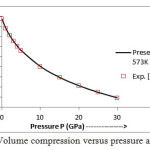Figure 7: Volume compression versus pressure at T=573 K.   Click here to View table

 

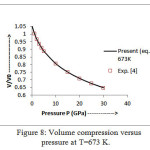Figure 8: Volume compression versus pressure at T=673 K.   Click here to View table

 

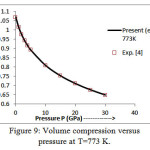Figure 9: Volume compression versus pressure at T=773 K.   Click here to View table

 

References

1. Schiotz, J.;Ditolla, F.D.; Jacobsen,K.W.Nature. 1998, 391, 561-563.
   CrossRef
2. Chidambaram R.; Sharma, S.M.Current Science.  1991, 60,397–408.
3. Wilson, B.;Dewers, T.;Reches, Z.;Brune, J.N.Nature. 2005, 434, 749–752.
   CrossRef
4. Anderson, O.L.Equation of state for Geophysics and Ceramic Science, (Oxford University Press, Oxford) 1995.
5. Kumar M., Kumar M. Indian J Pure App. Phys.2008, 46, 378.
6. Kushwah, S.S.; Srivastava, H.C.; Singh, K.S.Physica B 2007, 388, 20.
   CrossRef
7. Devlal, K.; Gupta, B.R.K.Pramana- J. of Physics 2007, 69, 307.
8. Kumar M. Indian J Pure App. Phys. 2001, 40, 202-206.
9. Kumar M.J. of Physics and Chemistry of solids 2004, 65, 1177.
10. Sorot,N.; Gupta,B.R.K.Orient. J. Chem.2015, 31 (3), 1327.
    CrossRef
11. Marcondes, M.L.;Wentzcovitch, R.M. J Applied Physics2015,117,215902.
    CrossRef
12. Kushwaha S. S., Shanker J. J PhysChem Solids 1998,59, 197.
    CrossRef
13. Singh D, Kumar S., Singh B.P. Indian J Pure App. Phys.2007, 45, 721-725.
14. Fang Z.H. High temperatures-high pressures1999, 31,507-510.
    CrossRef
15. Fang Z.H. J Applied Physics2007,102,article ID 013523.
16. Kumar M.PhysicaB: Physics of condensed matter1995,205,175-179.
17. Strassle,T.;Klotz, S.;Kunc,K.; Pomjakushin, V;White., J.S.Phys. Rev. B,2014, 90,014101.
18.  Matsui,M.;Higo, Y.;Okamoto, Y.;Irifune, T.; Funakoshi, K.Am. Mineral, 2012, 97,1670.
    CrossRef
19. Suzuki I. J. Phys. Earth 1975, 23, 145.
    CrossRef
20. Suzuki, I.;Okajima, S.; Seya, K. J. Phys. Earth 1979, 27, 63.
    CrossRef
21. Goyal, M; Gupta,B.R.K.High temperatures-high pressures2016,45, 163-177.
22. Born, M; Huang, K. Dynamical theory of crystal lattices,(Oxford University Press, Oxford) 1954.
23. Shanker, J.; Kumar, M.Phys. Status Solidi B1993,179, 351-356.
    CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.