Classification of Zintl Ion Clusters using 4n Series Approach
Enos Masheija Rwantale Kiremire
Department of Chemistry and Biochemistry, University of Namibia Private Bag 13301, Windhoek, Namibia.
*Corresponding Author E-mail: kiremire15@yahoo.com
DOI : http://dx.doi.org/10.13005/ojc/320401
Article Received on :
Article Accepted on :
Article Published : 11 Aug 2016
Zintlion clusters have the industrial potential for possible applications. A good understanding of such clusters in terms of their bonding, structures and chemical reactivity is extremely important. This paper attempts to categorize and predict the shapes of Zintl clusters of simple to medium nuclearity using the 4n series method.
KEYWORDS:Zintl ion; clusters; series; capping; encapsulated; fragment
Download this article as:| Copy the following to cite this article: Kiremire E. M. R. Classification of Zintl Ion Clusters using 4n Series Approach. Orient J Chem 2016;32(4). |
| Copy the following to cite this URL: Kiremire E. M. R. Classification of Zintl Ion Clusters using 4n Series Approach. Orient J Chem 2016;32(4). Available from: http://www.orientjchem.org/?p=20531 |
Introduction
Zintl ion clusters are normally generated by the reactions between alkali and alkaline earth elements in anhydrous liquid ammonia or ethylenediamine1. They are found to possess polyhedral geometries like boranes or metal carbonyl clusters and Wade-Mingos rules are utilized to categorize and predict their shapes2-3.Zintl phases are currently being investigated for potential industrial applications4. Therecently developed 4n series method has also been found to categorize clusters and predict shapes of small to medium clusters quite successfully5-6. However, the method has not been applied to analyze Zintl ion clusters in a systematic manner. The aim of this paper is to categorize and predict the shapes of Zintl clusters using the 4n series method.
Results and Discussion
The background of using the 4n series method
The 4n series method has been discussed in details in earlier work7-8. Nonetheless, a brief outline of the method will be given here as well as some examples illustrating of how it is applied. The 4n method involves the breaking down the cluster formula into mono-skeletal fragments. If it is a main group fragment, it must comprise of [4] skeletal valence electrons. A carbon atom [C] or borane fragment [BH] exactly fulfill this requirement. Thus,
1[C] →1[4] →1[4+0] = 1[4n+0](n=1)→ S = 4n+0(n=1).
If we have 2 carbon fragments, 2[C], then the result is doubled as follows:
2[C] →2[4]= 2[4+0] = 2[4n+0] → S = 4n+0(n=2).
If we have x[C] fragments, then ; x[C] = x[4+0] → S=4n+0(n=x).
If a fragment has more than 4 valence electrons, then the extra electrons are expressed as a digit after 4n. Let us take the example of a 1[CH] fragment.
1[CH]→1[4+1] =1[4n+1]→S =4n+1(n=1); the valence electron content of the fragment V = 4(1)+1 = 5.
2[CH]→2[4+1] =2[4n+1]→S = 4n+2(n=2); V = 4(2)+2 = 10, the valence electron content of 2[CH] fragments.
What matters most in the 4n series method is the skeletal element and the valence electron density around it. For instance, a phosphorus fragment, 1[P] with 5 valence electrons is treated in the same way as a 1[CH] fragment which is isolobal to it.
Hence, 1[P] = 1[5]→1[4+1] = 1[4n+1]→4n+1(n=1); for 2[P] =2[4+1] →2[4n+1]→S = 4n+2(n=2). We can use the series formula S = 4n+2(n=2) to derive a corresponding hydrocarbon as in
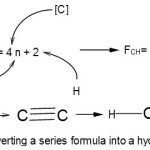 |
Scheme 1: Converting a series formula into a hydrocarbon Click here to View Scheme |
The skeletal bonds linking up the two carbon atoms is given by k = 2n-1 and since n =2, k =2(2)-1 = 3. Since P2 belongs to the same series S = 4n+2(n=2), k =2n-1 = 2(2)-1 = 3. Hence P2 is linked by a triple bond P≡P.
Consider a [CH2] fragment. The fragment has 6 valence electron content. These are converted into series as follows:
1[CH2]→1[4+2] →S = 4n+2(n=1). Let us see how two such fragments can be transmuted into series formula.
2[CH2]→2[4+2]→2[4n+2] →S = 4n+4(n=2). The corresponding hydrocarbon FCH = C2H4. We know that C2H4 has a double bond(C=C). Again the double bond can be derived from the series S = 4n+4; k = 2n-2 = 2(2)-2 = 2. In general, for series of the formula S = 4n+q, k = 2n-(q/2).
A sulphurflagment,1[S] alone also has 6 valence electrons like 1[CH2]. The 4n series method treats 1[S] as [CH2]. Thus, 1[S]⥈1[CH2]; the two fragments are isolobal. Hence,
1[S] →1[6] =1[4+2]→4n+2(n=1).
2[S]→2[4+2] →2[4n+2] = 4n+4(n=2). The electron valence content of 2[S] is given by V = 4n+4 = 4(2)+4 = 12. Also the k value of S2→k = 2n-2 = 2(2)-2 = 2. Hence, according to the series, the S2 molecule is doubly bonded (S=S) as in C2H4. In general, for a series formula S = 4n+q, the corresponding k value is given by k = 2n-(q/2).
Categorization of Clusters
The categorization of clusters is easily done using 4n rather than 14n series. Although this has already been discussed in earlier work,it is being summarized here as many readers are not familiar with the 4n series method of categorizing clusters. The categorization follows the sequence (lower series): S = 4n+2(closo), 4n+4(nido), 4n+6(arachno), 4n+8(hypho) and 4n+10(klapo) and so on. The (higher series) are the capping series namely, S = 4n+0(mono-capped), 4n-2(bi-capped), 4n-4(tri-capped), 4n-6(tetra-capped), 4n-8(penta-capped), 4n-10(hexa-capped) and so on. Since the work on 4n series method is beginning to expand, the terms ‘lower series’ and ‘higher series’ are being proposed to refer to non-capping and capping series respectively. It is proposed that the digit after ‘4n’ be referred to as a ‘determinant’ of the series since it gives an indication of the type of cluster or fragment.
When a transition metal fragment is involved, the relationship 14n+q⥈4n+q is applied. The 14n+q refers to the transition metal cluster series and 4n+q refers to main group cluster series. It has been found easier to work with 4n+q series rather than 14n+q series. The two series has been found to obey the Hoffmann’s isolobal relationship9,5. This means that if we have a cluster comprising of skeletal elements from transition and main group elements, the valence electron content of a transition metal are transformed into those of the corresponding main group skeletal element. Let us look at a couple of examples.
1[Os(CO)3 ]→ 1[8+6]=1[14+0]→1[14+0-10]=1[4+0]→S = 4n+0(n=1).
1[Os(CO)4]→1[8+8] = 1[14+2] →1[14+2-10]=1[4+2]→S=4n+2(n=1)
1[Os(CO)5]→1[8+10]=1[14+4]→1[14+4-10]= 1[4+4] →S = 4n+4(n=1)
Derivation of Series Formula of Zintl ion Clusters
Sn52―
5[Sn]→5[4+0]→4n+0(n=5)
q→0+2(n=0)
S = 4n+2(n=5), Closo cluster; k =2n-1=2(5)-1 =9.
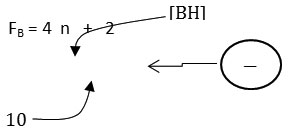
The equivalent borane cluster, FB = 4n+2 = [BH](5)+2(-) = B5H52― for closo system. The cluster will be expected to have a similar shape as B5H52―. The sketch of ideal predicted shape trigonalbipyramid is shown in F-1.
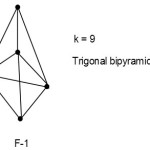 |
Figure 1 Click here to View Figure |
Bi3Cr2(CO)63―
3[Bi] →3[4+1] →4n+3(n=3)
2[Cr(CO)4]→2[14+0]→2[14+0-10]=2[4+0]→4n+0(n=2)
[6-8](CO) = – 2(CO)→0-4(n=0)
q→0-3(n=0)
S = 4n-4(n=5), Cp = C3C[M-2]; tri-capped cluster.
Si4(CuR)24―
4[Si]→4[4+0] →4n+0(n=4)
2[CuRH2]→4n+0(n=2)
[0-4](H) = -4H→0-4(n=0)
q→0+4(n=0)
S =4n+0(n=6), mono-capped series, Cp = C1C[M-5]. This is a mono-capped trigonal bipyramid.
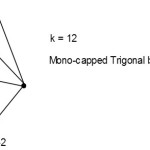 |
Figure 2 Click here to View Figure |
Pb5G24―; G = Mo(CO)3
5[Pb] →5[4+0] →4n+0(n=5)
2[Mo(CO)4]→4n+0(n=2)
[6-8](CO) = – 2(CO)→0-4(n=0)
q→0+4(n=0)
S = 4n+0(n=7); Cp = CIC[M-6]. Thus, the series predicts a mono-capped octahedral cluster.
As73―
7[As]→7[4+1] →4n+7(n=7)
q→0+3(n=0)
S=4n+10(n=7) ; k =2n-5 = 2(7)-5 =9. A skeletal sketch is shown in F-3A.
 |
Figure 3a Click here to View Figure |
Bi3Ni4(CO)63―
3[Bi] →3[4+1] →4n+3(n=3)
4[Ni(CO)2]→4n+0(n=4)
[6-8](CO) = – 2(CO)→0-4(n=0)
q→0+3(n=0)
S = 4n-4(n=7), Cp = C3C[M-4]; tri-capped tetrahedral cluster.
Bi3Ni6(CO)93―
3[Bi] →3[4+1] →4n+3(n=3)
6[Ni(CO)2]→4n+0(n=6)
[9-12](CO) = – 3(CO)→0-6(n=0)]
q→0+3(n=0)
S = 4n-6(n=9)(n=9); Cp = C4C[M-5]; tetra-capped cluster.
In4Bi53―
4[In] →4[4n-1]= 4n-4(n=4)
5[Bi]→5[4+1]=4n+5(n=5)
q→0+3(n=0)
S = 4n+4(n=9); Nido cluster, FB = 4n+4 = [BH](9)+4(H) = B9H13. The nido cluster is derived from B10H102― following Rudolph correlation system10. This is graphically represented in F-3B below.
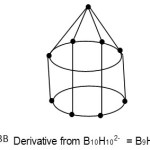 |
Figure 3b Click here to View Figure |
Si9(ZnPh)3―
9[Si] →9[4+0]→ 4n+0(n=9)
1[ZnPh(H)]→1[14+0]→1[14+0-10] = 1[4+0]→ 4n+0(n=1)
[0-1](H)→ 0-1(n=0)
q→ 0+3(n=0)
S = 4n+2(n=10), closo cluster; k =2n-1 =2(10)-1 = 19.
FB = 4n+2 = [BH](10)+2(-1) = B10H102― for closo system. The cluster is predicted to have a shape similar to that of B10H102―cluster. This is graphically represented by the skeletal sketch F-4. The shape resembles a beautiful doubly closed basket. One end of the closed tip resides the Zn skeletal element.
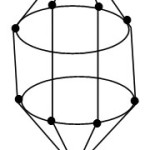 |
Figure 4 Click here to View Figure |
Sn9Cr(CO)34―
9[Sn]→9[4+0]→4n+0(n=9)
1[Cr(CO)4]→4n+0(n=1)
[3-4](CO) = – 1(CO)→0-2(n=0)
q→0+4(n=0)
S = 4n+2(n=10), Closo cluster; FB = B10H102―. Cluster expected to have a similar shape as B10H102―.
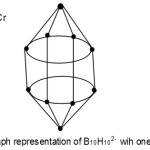 |
Figure 5 Click here to View Figure |
Sn9IrL23―
9[Sn]→4n+0(n=9)
1[IrHL2]→4n+0(n=1)
[0-1](H) = – 1(H)→0-1(n=0)
q→0+3(n=0)
S = 4n+2(n=10), Closo
Shape predicted to be similar to that of B10H102―.
Sn9W(CO)34―
9[Sn]→9[4+0]→4n+0(n=9)
1[W(CO)4]→4n+0(n=1)
[3-4](CO) = – 1(CO)→0-2(n=0)
q→0+4(n=0)
S = 4n+2(n=10), Closo cluster; FB = B10H102―. Cluster expected to have a similar shape as B10H102―. Isomerism occurs in this case as W now occupies the equatorial position.
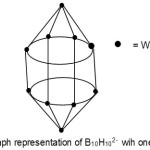 |
Figure 6 Click here to View Figure |
Sn9IrL23―
9[Sn]→4n+0(n=9)
1[IrHL2]→4n+0(n=1)
[0-1](H) = – 1(H)→0-1(n=0)
q→0+3(n=0)
S = 4n+2(n=10), Closo
Shape predicted to be similar to that of B10H102―.
Pb102―
10[Pb]→4n+0(n=10)
q→0+2(n=0)
S =4n+2(n=10), Closo clusterFB = [BH](10)+2(-1) = B10H102―.The negative charge is added since the system is closo. The graphical representation is shown below.
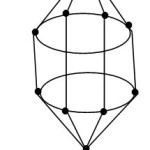 |
Figure 7 Click here to View Figure |
Ni@Pb102―
1[Ni] →1[10] = 1[14-4]→1[4n-4] = 4n-4(n=1)
10[Pb]→10[4n+0]→4n+0(n=10)
q→0+2(n=0)
S = 4n-2(n=11), Cp = C2C[M-9]
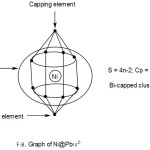 |
Figure 8 Click here to View Figure |
Ni@Pb122―
1[Ni] →1[10] = 1[14-4]→1[4n-4] = 4n-4(n=1)
12[Pb]→12[4n+0]→4n+0(n=12)
q→0+2(n=0)
S = 4n-2(n=13), Cp = C2C[M-11]. This means 2 of the 13 skeletal elements are capped around the remaining 11 others. This could imply the inner set of [5:1:5] skeletal elements as shown in F-9.
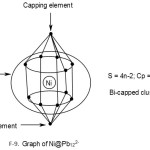 |
Figure 9 Click here to View Figure |
Ni2Sn174―
2[Ni]→2[10]=2[14-4] →2[14-4-10]= 2[4n-4]→4n-8(n=2)
17[Sn] →17[4+0]→17[4n+0] →4n+0(n=17)
q→0+4(n=0)
S = 4n-4(n=19)→Cp = C1+C2 →C3C[M-16]
According to the 4n series, the cluster is tri-capped. This implies, 3 skeletal atoms are capping versus 16 ones which are not capping. A possible skeletal shape consistent with this prediction in sketched graphically below. Thus, the 2 nickel atoms are regarded as capping in addition to one of the 17 Sn skeletal elements that acts as a bridge of two Sn8 fragments. This is sketched in F-10.
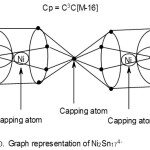 |
Figure 10 Click here to View Figure |
General considerations
A wide range of small to medium nulearity Zintl ion clusters taken from several sources11-14have been analyzed and categorized using 4n series method. The results are summarized in Table 1. The common Zintl ion clusters belong to the clusters series S = 4n+6, 4n+4 and 4n+2. They comprise of skeletal elements ranging from two (M-2) to thirteen (M-13). As can be seen from Table 1, capping series as defined by 4n series method are not common. But capping may be induced if a capping fragment is introduced into a cluster. The capping fragment is usually a transition metal atom with ligands or a metal atom or a main group element such as aluminum (Al). A good example of a capping fragment is M(CO)3, M = Cr, Mo, and W. The valence content V of the fragment = 12 = 14-2. Hence, it belongs to the series S = 14n-2 ⥈4n-2 series. If Sn94― belongs to S = 4n+4(nido) and M(CO)3 belongs to S =4n-2(capping series), then Sn94―+ M(CO)3→ Sn9[M(CO)3]4― and net S = (4n+4)+(4n-2) = 4n+2(closo). This means that the nido cluster has been transformed into a closo cluster by adding the capping fragment. The nido cluster S = 4n+4(n=9), corresponds to an equivalent borane FB =B9H13 while the closo corresponds to an equivalent closo borane S =4n+2(n=10), FB= B10H102―. The capping fragment, M(CO)3 corresponds to adding (+B, -H) or [BH]2+ fragment to B9H13 cluster. Other good capping fragments are Ni(CO), S = 4n-2, and PtL, L =PPh3, S = 4n-2. Other fragments, M(CO)2, M = Fe, Ru, Os which have a content of 12 valence electrons could be good candidates.
Addition of a metal atom to a closo cluster, may generate a capped cluster. For instance, a nickel atom, [Ni] has 10 valence electrons. According to series it belongs to 14-4 →S = 14n-4 ↭4n-4. Therefore it has a capping influence when it is encapsulated in a cluster. For instance, Pb102―(S = 4n+2)+Ni(S =4n-4)→Ni@ Pb102―(S=4n-2).Thus, the encapsulated cluster becomes a bi-capped cluster, Cp = C2C[M-9]. This implies the [M-9] closo nucleus comprises of 9 atoms arranged as 4:1:4 capped by 2 atoms one on one side of the nucleus and the remaining on the other. The whole structure resembles a doubly closed basket as indicated in the sketched graph for 2.2.15. The encapsulated Zintl cluster Ni@Pb122― can be analyzed in the same way and it is found to belong to the same bi-capped series, S = 4n-2 and Cp = C2C[M-11]. This means that 2 skeletal atoms are capping on 11 others. The [M-11] closo atoms are observed to be organized in an approximate order [5:1:5]. The entire doubly closed basket-like closed structure has a skeletal atom arrangement 1:[5:1:5]:1. This arrangement is shown in a graphical skeletal sketch in 2.2.16 above.
Table 1: Categorization of Zintl Ion Clusters
|
CLUSTER |
SERIES |
n VALUE |
CATEGORY SERIES |
BORANE |
HYDROCARB |
k VALUE |
|
Bi22― |
4n+4 |
2 |
Nido |
B2H6 |
C2H4 |
2 |
|
Bi33― |
4n+6 |
3 |
Arachno |
B3H9 |
C3H6 |
3 |
|
Sb33― |
4n+6 |
3 |
Arachno |
B3H9 |
C3H6 |
3 |
|
As33― |
4n+6 |
3 |
Arachno |
B3H9 |
C3H6 |
3 |
|
Ge34― |
4n+4 |
3 |
Nido |
B3H7 |
C3H4 |
4 |
|
Ga3R32― |
4n+2 |
3 |
Closo |
B3H5 |
C3H2 |
5 |
|
Bi42― |
4n+6 |
4 |
Arachno |
B4H10 |
C4H6 |
5 |
|
Pb2Sb22― |
4n+4 |
4 |
Nido |
B4H8 |
C4H4 |
6 |
|
Sn2Bi22― |
4n+4 |
4 |
Nido |
B4H8 |
C4H4 |
6 |
|
Ge44― |
4n+4 |
4 |
Nido |
B4H8 |
C4H4 |
6 |
|
Pb44― |
4n+4 |
4 |
Nido |
B4H8 |
C4H4 |
6 |
|
Sn44― |
4n+4 |
4 |
Nido |
B4H8 |
C4H4 |
6 |
|
InBi32― |
4n+4 |
4 |
Nido |
B4H8 |
C4H4 |
6 |
|
Tl2Te22― |
4n+2 |
4 |
Closo |
B4H42― |
C4H2 |
7 |
|
Al42― |
4n-2 |
4 |
C2C[M-2] |
B4H2 |
C4-2H |
9 |
|
Bi55― |
4n+10 |
5 |
Klapo |
B5H15 |
C5H10 |
5 |
|
Bi3Cr2(CO)63― |
4n+2 |
5 |
Closo |
B5H52― |
C5H2 |
9 |
|
Pb52― |
4n+2 |
5 |
Closo |
B5H52― |
C5H2 |
9 |
|
Sn52― |
4n+2 |
5 |
Closo |
B5H52― |
C5H2 |
9 |
|
Si4(CuR)24― |
4n+0 |
6 |
C1C[M-5] |
B6H6 |
C6 |
12 |
|
Bi3Ni4(CO)63― |
4n+2 |
7 |
Closo |
B7H72― |
C7H2 |
13 |
|
As73― |
4n+10 |
7 |
Klapo |
B7H17 |
C7H10 |
9 |
|
Pb2Fe3 Cr2(CO)192― |
4n+6 |
7 |
Arachno |
B7H13 |
C7H6 |
11 |
|
Pb2Fe5(CO)172― |
4n+6 |
7 |
Arachno |
B7H13 |
C7H6 |
11 |
|
Pb5Mo2(CO)64― |
4n+0 |
7 |
C1C[M-6] |
B7H7 |
C7 |
14 |
|
Sn86― |
4n+6 |
8 |
Arachno |
B8H14 |
C8H6 |
13 |
|
Bi4Ni4(CO)62― |
4n+2 |
8 |
Closo |
B8H82― |
C8H2 |
15 |
|
Si94― |
4n+4 |
9 |
Nido |
B9H13 |
C9H4 |
16 |
|
Si93― |
4n+3 |
9 |
Free radical |
B9H12 |
C9H3 |
16.5 |
|
Ge93― |
4n+3 |
9 |
Free radical |
B9H12 |
C9H3 |
16.5 |
|
Ge94― |
4n+4 |
9 |
Nido |
B9H13 |
C9H4 |
16 |
|
Sn94― |
4n+4 |
9 |
Nido |
B9H13 |
C9H4 |
16 |
|
In4Bi53― |
4n+4 |
9 |
Nido |
B9H13 |
C9H4 |
16 |
|
Tl4Bi53― |
4n+4 |
9 |
Nido |
B9H13 |
C9H4 |
16 |
|
In5Bi45― |
4n+4 |
9 |
Nido |
B9H13 |
C9H4 |
16 |
|
Ge92― |
4n+2 |
9 |
Closo |
B9H92― |
C9H2 |
17 |
|
TlSn83― |
4n+2 |
9 |
Closo |
B9H92― |
C9H2 |
17 |
|
Tl5Sb43― |
4n+2 |
9 |
Closo |
B9H92― |
C9H2 |
17 |
|
Tl6Sb35― |
4n+2 |
9 |
Closo |
B9H92― |
C9H2 |
17 |
|
Sn92― |
4n+2 |
9 |
Closo |
B9H92― |
C9H2 |
17 |
|
TlSn93― |
4n+2 |
10 |
Closo |
B10H102― |
C10H2 |
19 |
|
Si9(ZnPh)3― |
4n+2 |
10 |
Closo |
B10H102― |
C10H2 |
19 |
|
Sn9 Cr(CO)34― |
4n+2 |
10 |
Closo |
B10H102― |
C10H2 |
19 |
|
Sn9 W(CO)34― |
4n+2 |
10 |
Closo |
B10H102― |
C10H2 |
19 |
|
Pb9 Mo(CO)34― |
4n+2 |
10 |
Closo |
B10H102― |
C10H2 |
19 |
|
*Sn9 IrL23― |
4n+2 |
10 |
Closo |
B10H102― |
C10H2 |
19 |
|
Ge9 Ni(CO)34― |
4n+1 |
10 |
Free radical |
B10H11 |
C10H1 |
19.5 |
|
Bi3Ni6(CO)93― |
4n+0 |
9 |
C1C[M-8] |
B9H9 |
C9 |
18 |
|
**Ge9CuL3- |
4n+0 |
10 |
C1C[M-9] |
B10H10 |
C10 |
20 |
|
Ge9PdL3― |
4n-2 |
10 |
C2C[M-10] |
B10H8 |
C10-2H |
21 |
|
In10Zn8― |
4n-4 |
11 |
C3C[M-8] |
B11H7 |
C11-4H |
23 |
*L2 = COD, **L =Ph
|
Sn6Cr6(CO)302― |
4n+14 |
12 |
– |
B12H26 |
C12H14 |
17 |
|
Sn1212― |
4n+12 |
12 |
– |
B12H24 |
C12H12 |
18 |
|
Ge122― |
4n+2 |
12 |
Closo |
B12H122― |
C12H2 |
23 |
|
Tl1311― |
4n-2 |
13 |
C2C[M-11] |
B13H11 |
C13-2H |
27 |
|
Ga6Sb814― |
4n+16 |
14 |
– |
B14H30 |
C14H16 |
20 |
|
ZnAs144― |
4n+16 |
15 |
– |
B15H31 |
C15H16 |
22 |
|
Ni2Sn174― |
4n-4 |
19 |
C3C[M-16] |
B19H15 |
C19-4H |
40 |
|
*Ga19X6― |
4n-12 |
19 |
C7C[M-12] |
B19H7 |
C19-12H |
44 |
|
(Si9)2[Ni(CO)2]28― |
4n+8 |
20 |
Hypho |
B20H28 |
C20H8 |
36 |
|
Ga26G82― |
4n-16 |
26 |
C9C[M-17] |
B26H10 |
C26-16H |
60 |
*X = CR3 , R =SiMe3
Conclusion
The 4n series method has been shown to be successful in analyzing, categorizing transition metal carbonyl, boranes, heteroboranes and hydrocarbon clusters. In this paper, it has been demonstrated that it can also readily be applied mainly to the categorization and structural prediction of small to medium size Zintl ion clusters. It is hoped that it may be applied to the analysis and categorization of large Zintl clusters.
Acknowledgement
I wish to extend my gratitude to the University of Namibia for providing facilities and financial support. NAMSOV, Namibia is also acknowledged for generous financial support and Mrs Merab Kambamu Kiremire for her continued encouragement to write the articles.
References
- Scharfe, S., Kraus, F., Stegmaier, S., Fässler, T. F.,Angew., Chem., Int., And., 2011, 50, 3630-3670.
- Wade, K., J. Chem. Soc., Dalton, 1971, 792-793.
- Mingos, D. M. P., Nature Physical Science, 1972, 236, 99-102.
CrossRef - Kauzlarich, S. M., Brown, S. R.,Snyder, G. J., J. Chem. Soc., Dalton, 2007,2099-2107.
- Kiremire, E. M., Orient. J. Chem., 2015,31(Spl. Edn), 59-70.
- Kiremire, E. M., Orient. J. Chem., 2015,31(2), 605-618.
CrossRef - Kiremire, E. M. R., Int. J. Chem., 2016, 8(1), 145-158.
CrossRef - Kiremire, E. M. R., Int. J. Chem., 2016,8(1), 126-144.
CrossRef - Hoffmann, R., Angew., Chem., Int., Edn, 1982,21(10),711-800.
- Rudolph, R. W.,Acc. Chem. Res., 1976,9(12), 446-452.
CrossRef - Sevov, S. C., 2008,www3.nd.edu.sevovlab/articles/c02-6-1. Downloaded 03-07-2016.
- Goicoechea, J. M., Sevov,S. C.,J. Am. Chem. Soc., 2004,126,6860-6861.
CrossRef - Hull, M. W., Sevov, S. C., Angew., Chem., Int. Edn., 2007,46, 6695-6698.
CrossRef - Goicoechea, J. M., Sevov,S. C.,Organomet., 2006,25,4530-4536.
CrossRef

This work is licensed under a Creative Commons Attribution 4.0 International License.









