Characterization of Quaternary Chalcogenide As-Ge-Te-Si Thin Films

Introduction

Chalcogenide glasses are a recognized group of inorganic glassy materials which always contain one or more of the chalcogen elements S, Se, or Te but not O, in conjunction with more electropositive elements as As, Sb, and Bi. Chalcogen glasses are generally less robust, weakly bonded materials than oxide glasses.

Initially, glasses containing chalcogen elements were the subject of study owing to their interesting semiconducting properties, and more recently for their applications in optical recording [1, 2], technological applications, like optical imaging or storage media [3] and in the field of infrared optical transmitting materials, fiber optics and memory devices  [4]. The absence of long-range order of chalcogenide glassy semiconductors allows the modification of their optical properties to a specific technological application by continuously changing their chemical composition [5, 6]. Hence the study of the dependence of the optical properties on composition is important to improve technological application [7, 8]. As chalcogenide glassy semiconductors, the physical properties of As-Te-Si and Ge-Te-Si are strongly dependent on composition, thus composition is especially importance in studying their physical properties. In fact the chemical bond approach was very useful in predicting the semiconductor properties of different compounds and crystal classes [9]. The present study investigates the influence of the addition of Si (0, 5, 10, 12 and 20 at %), which is lower in atomic weight than Te, on the optical properties of new, amorphous As₃₀Ge₁₀Te_60-xSi_x thin films. In addition, the optical band gap (E_g), the average coordination numbers (N_co) and the average heat of atomization (H_s) of the As₃₀Ge₁₀Te_60-xSi_x glasses have been examined theoretically. The results were interpreted in terms of the chemical bond approach used to estimate the cohesive energies of the glasses under investigation.  

Experimental details

Different compositions of bulk As₃₀Ge₁₀Te_60-xSi_x  (where x = 0, 5, 10, 12, 20 at %) chalcogenide glasses  were prepared from high-purity (99.999%) As, Ge, Te and Si by the melt-quench technique. Appropriate proportions of the raw materials were weighted and sealed into silica ampoules under a vacuum of ≈10^-4 Pa, which were then heated gradually up to a temperature of 1125 K within 1 h and kept constant for 8 h. Throughout the heating process the ampoules were regularly shaken to ensure homogeneity and then quenched in ice-cold water to avoid crystallization.

Thin films of As₃₀Ge₁₀Te_60-xSi_x were prepared by thermal evaporation of the bulk samples. The thermal evaporation process was performed inside a coating (Edward 306E) system at a pressure of approximately 10^-4Pa. During the deposition process (at normal incidence), the substrates were suitably rotated to obtain films of uniform thickness. Film thickness was controlled in the range 100-200 nm using a quartz crystal (Edward FTM5) thickness monitor. The elemental compositions of the investigated specimens were checked using the energy dispersive X-ray (Link Analytical Edx) spectroscopy. Deviations in the elemental composition of the evaporated thin films from the initial bulk specimens did not exceed 1.0 at %. The amorphous state of the films was checked using an x-ray diffractometer (Philips type 1710 with Cu as a target and Ni as a filter; λ = 1.5418 Ǻ). The absence of crystalline peaks confirmed the glassy state of the prepared samples. A double beam (Shimadzu 2101 UV-VIS) spectrophotometer was used to measure reflectance and transmittance for the prepared films in the spectral wavelength range 200-1100 nm. 

Simulation Results and Discussion

Loffe and Regel [10] have suggested that the bonding character in the nearest neighbor region, which is the coordination number (the degree of cross linking), characterizes the electronic properties of the semiconducting materials. It is well known that the coordination number of covalently bonded atoms in glass is given by the so called 8-N rule, where N is the number of outer-shell electrons [11]. The numbers of the nearest neighbor atoms for As, Ge, Te and Si are calculated and listed in Table 1.

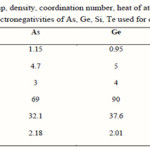Table 1 Click here to View table

 

The average coordination number which is defined simply as the atom-averaged covalent coordination of the constituents [12]. In the quaternary compounds A_αB_βC_γD_λ the averaged coordination number is generalized as:

For our compound the average coordination number is give by the following 2^nd relation [13]

The degree of cross linking has a profound effect on the thermal and mechanical properties of chalcogenide glasses, because increasing the cross linking makes the atoms become more tightly bound [14]

The determination of N_CO allows the estimation of the number of constraints (N_S). This parameter is closely related to the glass-transition temperature and associated properties. For a material with coordination number  N_CO, N_S can be expressed as the sum of the radial and angular valence force constraints [15]:

The calculated values of Nco and Ns for the As₃₀Ge₁₀Te_60-xSi_x  system are given in Table 2. The parameter r, which determines the deviation of stoichiometry and is expressed by the ratio of the covalent bonding possibilities of chalcogen atoms to that of non-chalcogen atoms, was calculated using the following relation [16, 17]:

The calculated values of r for As₃₀Ge₁₀Te_60-xSi_x system are given in Table 2.

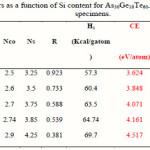Table 2 Click here to View table

According to Pauling [18], the heat of atomization Hs(A-B) at standard temperature and pressure of a binary semiconductor formed from atoms A and B is the sum of the heats of formation ΔH and the average of the heats of atomization H^A_S   and H^B_S   corresponding to the average non-polar bond energy of the two atoms [19, 20]:

ΔH proportional to the square of the difference between the electronegativities χA and χB of the two atoms:

ΔH that is strongly correlated with the difference in the ionicities of different atoms is small compared to the cohesive energy because the electronegativities of the constituent elements such as As, Te, Si are very similar. In most cases the heat of formation of chalcogenide glasses is unknown. In the few materials for which it is known, the heat of formation ΔH is about 10% of the heat of atomization and, therefore, can be neglected.

To extend the idea to ternary and higher order semiconductor compounds, the average heat of atomization is defined for a compound A_αB_βC_γD_λ as [21, 22]:

The values of H_s for As₃₀Ge₁₀Te_60-xSi_x alloys, obtained using the values of  H_s of As, Ge, Te and Sb are given in Table 2. As shown in Table 2, the values of H_s increase with increasing Si Content. To correlate  H_s with Eg in non-crystalline solids, it is reasonable to use the average coordination number instead of the isostructure of crystalline semiconductors.

It was found that the variation in the theoretical values of the energy gap (Eg,th) with composition in quaternary alloys can be described [23] by the following simple relation:

Where Y is the volume fraction of element. For quaternary alloys:

Where a, b, c and d are the volume fractions of the elements A, B, C and D, respectively. Are the corresponding optical gaps. The conversion from a volume fraction to atomic percentage is made using the atomic weights and densities [24] tabulated in Table 1. The calculations of Eg,th, based on the above equation for the As₃₀Ge₁₀Te_60-xSi_x alloys, are given in Table 2, which reveal that the addition of Si leads to a change in the considered properties. The increase in Si leads to increase in Eg,th and Nco. The various bond energies of the expected bonds in the system are listed in Table 3. By increasing the Si content, the average bond strength of the compound decreases and hence E_g will decrease.

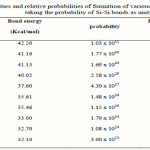Table 3 Click here to View table

To emphasize the relationship between Eg and the average bond strength more clearly, Eg is compared with Hs/Nco which is the average single-bond energy in the alloy. One observes that Eg, as well as Hs/Nco increase with increasing Si content, which suggests that one of the main factors determining Eg is the average single bond in the alloy [25]. Fig. 1 shows the x-ray diffraction patterns for As₃₀Ge₁₀Te_60-xSi_x thin films. The absence of diffraction lines in the x-ray patterns indicates that the films have amorphous structures. Transmission spectra, corresponding to the amorphous As₃₀Ge₁₀Te_60-xSi_x thin films before and after radiation of 1 and 15 mega rad, are plotted in figs. 2, 3 and 4 show a clear ultraviolet shift of the interference-free region with increasing Si content.

The values of the absorption coefficient (α) for the studied films were calculated from transmittance T and reflectance R using the equation:

Where d is the thickness of the film. According to Tauc’s relation [26, 27] for the allowed non-direct transition, the photon energy dependence of the absorption coefficient can be described by:

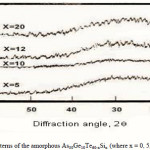Figure 1 Click here to View figure

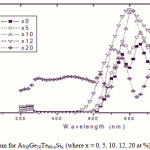Figure 2 Click here to View figure

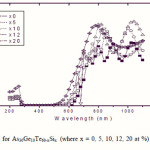Figure 3 Click here to View figure

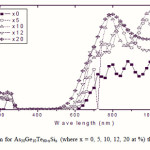Figure 4 Click here to View figure

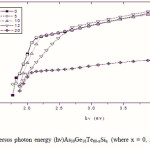Figure 5 Click here to View figure

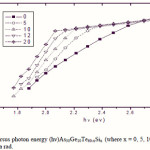Figure 6 Click here to View figure

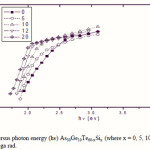Figure 7 Click here to View figure

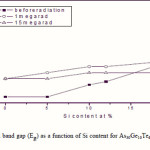Figure 8 Click here to View figure

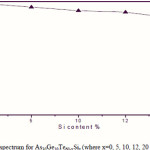Figure 9 Click here to View figure

Where B is a parameter that depends on the transition probability. Figs. 5, 6 and 7 are a typical best fit of (αhν)^1/2 versus photon energy (hν) for As₃₀Ge₁₀Te_60-xSi_x thin films before and after radiation of 1 and 15 mega rad. The intercepts of the straight lines with the photon energy axis give the values of the optical band gap. The variation in  Eg as a function of Si content before and after radiation of 1and 15 mega rad are shown in Fig. 8. It is clear that Eg increases with increasing Si content of the investigated films. Fig. 9 shows the density of amorphous As₃₀Ge₁₀Te_60-xSi_x thin film and it is clear that density decreases with increasing Si content.

The possible bond distribution at various compositions using chemically ordered network (CON) model [28]. This model assumes that: a) Atoms combine more favourably with atoms of different kinds than with the same and (b) bonds are formed in the sequence of bond energies. The bond energies D(A-B) for heteronuclear bonds have been calculated by using the empirical relation [29]:

Proposed by Pauling [30], where D(A-A) and D(B-B) are the energies of the homonuclear bonds (in units of Kcal/mol) [31]: χA and χB are the electronegatives for the involved atoms [32].

At elevated temperatures, energy bonding effects can influence the film composition. This is because more energy is available to the atoms striking a hot substrate and they can adjust themselves after striking to form more favorable (i.e higher energy) bonds. Thus, for the present material, more silicon might be incorporated into the films at higher temperatures because it is possible for silicon to form relatively strong bonds with other constituents. This hypothesis is supported by the contents of table (3) which lists the relative order of the bond energies of the ten possible bonds in the Si-Te-As-Ge system. The hetero-atom single-bond energies were calculated from the average of the homo-atom single-bond energies for silicon, tellurium, arsenic and germanium, with the addition of an ionic contribution proportional to the square of the electronegatives difference between the elements.

It can be seen from table (3) that silicon has a better chance of sticking to the growing film at elevated temperatures as it can form strong bonds with tellurium, the major constituent. However, the As-Te bonds are relatively weak so that a deficiency of arsenic might be expected on energetic grounds.

Knowing the bond energies, we can estimate the cohesive energy (CE),i.e. the stabilized energy of an infinitely large cluster of the material per atom, by  Summing the bond energies over all the bonds expected in the system under test  the CE of the prepared samples is evaluated from the following equation [33]

Where Ci and Di are the numbers of the expected chemical bonds and the energy of each corresponding bond, respectively. The calculated values of CE for all compositions are presented in table 2. CE increases with increasing Si content. Increasing the Si content leads to an increase in the average molecular weight, which increases the rigidity (strength) of the system.

To explain the electrical behaviour of amorphous systems. This approach explains the behaviour in terms of cohesive energy (CE). It allows the determination of the number of possible bonds and their type (heteropolar and homopolar). The energies of various possible bonds in the As-Ge-Si-Te system are given in table 3. Depending on the bond energy (D), the relative probability of its formation was calculated[34] using the probability function exp (D/kT) and listed in table 3. Bonds, such as Si-Si, Ge-Ge, Te-Te and As-As bonds exist with high priority in the As-Ge-Si-Te system.

Conclusions

Optical data indicated that the allowed, non-direct gap is responsible for photon absorption in As₃₀Ge₁₀Te_60-xSi_x thin films. Increasing Si content at the expense of Te atoms increasing the optical gap of the films. The values for heat of atomization, coordination number, number of constraints and cohesive energy of As₃₀Ge₁₀Te_60-xSi_x are dependent on the glass composition. The increase in Si content leads to increase in Eg,th, Hs/Nco and Nco. Cohesive energy increases with the increase in Si content. The chemical-bond approach can be applied successfully to interpret the increase in the optical gap with increasing Si content

Acknowledgement

The authors would like to thank Dr. A. Abdglel Solid State Physics Department, NationalCenter for Radiation Research and Technology, Atomic Energy Authority, Cairo, Egypt for his help and support.

References

1. N.A. Goryunova and B.T. Kolomiets, Zh. Tekhn. Fiz. 25 (1955) 984.
2. K. Tanaka, Y. Osaka, M.Sugi et al.,J. Non-Cryst. Solids 12 (1973) 100.
3. A. E. Owen, A. P. Firth and P. J. S. Ewen, Phil. Mag. B 52 (1985) 347.
4. R. Zallen, the Physics of Amorphous Soilds (Wiley, New York, 1983).
5. E. A. Davis, J. of  Non Cryst. Sol. (1985) 71, 113.
6. A.H. Moharram, A.A. Othman, H.H. Amer, et al., J. Non-Cryst. Solids 352 2187 (2006).
7. M.  Yamaguchi.Phil Mag 51 (1985) 651.
8. S. S. Fouad, A. Ammar, M. Abo-Ghazala, Pyscial B 229 (1997) 249.
9. E. Mooser, WB. Pearson, Prog Semicond 5 (1960) 103.
10. A.F. loffe and A.R. Regel, Prog. Semicond. 4 (1960) 239.
11. P. Kumar, K. Singh, Chalcogenide Letters Vol. 4,No. 11; (2007) 127.
12. A. K. Varshneya, A. N. Sreeram, D. R. Swiler, Physc. Chem. Glasses 34 (1992) 179
13. [13] S.S. Fouad, Vacuum 52 (1999) 505.
14. G. H. Frischat, U. Brokmeir, A. Rosskamp, J. of Non Crystalline Solids 50 (1982) 263.
15. A. Dahshan, K.A. Aly, Philosophical Magazine, Vol. 88, No. 3  (2008) 361.
16. L. Tichy and H. Ticha, Mater. Lett. 21  (1994) 313.
17. L. Tichy and H. Ticha, J.  Non-Cryst. Solids 189 (1995) 141.
18. Pauling L. J Phys Chem 1954;58:662; The nature of the chemical bond, New York: Cornell University Press, 1960.
19. S.A. Fayek and S.S. Fouad, Vacuum 52 (1998) 359.
20. Brewer L. Electronic Structure and Alloy Chemistry of the Transition Elements. Beck PA (editor), New York: Inter Science, 1963:222.
21. N.F. Mott, E.A, Davis, R.A. Street, Phil. Mag. 32 (1975) 961.
22. M. F. Thorpe, J. Non. Cryst. Solids 182 (1995) 135.
23. S.S. Fouad, Vacuum 52 (1999) 505.
24. S. Mahadevan, A. Giridhar and A.K. Singh, J. Non-Cryst. Solids 169 (1994) 133.
25. S.S. Fouad, A.H. Ammar and M. Abo-Ghazala, Vaccum 48 (1997) 181.
26. H . Fritzsche Philos. Mag. B 68  (1993) 561
27. A. Dahshan, H.H. Amer and K.A. Aly. J. Phys. D: Appl. Phys. 41 (2008) 215401.
28. S. R. Elliot, Physics of Amorphous Solids, Longman Inc, New York, 134 (1984).
29. P. Sharma, M. Vashistha and I. P. Jain Chalcogenide Letters Vol. 2, No. 11 (2005) 115.
30. L. Pauling, The Nature of the Chemical Bond, 3^rd ed (Cornell University Press, NY, 1960), P.91.
31. L. Tichy, A. Triska, H. Ticha, et al., SolidState Commun. 41 (1982) 751.
32. J. Bicermo and S.R. Ovshinsky, J. Non-Cryst. Solids 74 (1985) 75.
33. S.A. Fayek, J. Phys. Chem. Solids 62 (2001) 653.
34. D.R. Goyal and A.S. Maan, J. Non-Crys. Solids 183 (1995) 182.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.