A Unique Bypass to the Carbonyl Cluster ‘Nucleus’ Using the 14n Rule
Enos Masheija Kiremire
Department of Chemistry and Biochemistry, University of Namibia, Private Bag 13301, Windhoek, Namibia
DOI : http://dx.doi.org/10.13005/ojc/310326
Article Received on :
Article Accepted on :
Article Published : 29 Aug 2015
This paper introduces a method of classifying clusters of the transition metal carbonyls based on the 14n rule. It was derived from close analysis of the relationship between the number of skeletal atoms, valence electrons and eighteen electron rule in the case of transition elements, and the known bonds or linkages of simple clusters. The analysis reveals that there is an infinite range of carbonyl clusters. These clusters occur in an orderly manner forming definite series. In addition to the categorization of clusters, tentative assignment of geometries in particular those of simple ones can be predicted. Furthermore, the method is able identify the possible INNER CORE NUCLEAR CLUSTER of some large carbonyl clusters. This paper presents a highly refined and simplified new method of classifying carbonyl clusters.
KEYWORDS:Unique Bypass; method; classifying clusters; transition metal
Download this article as:| Copy the following to cite this article: Kiremire E. M. A Unique Bypass to the Carbonyl Cluster ‘Nucleus’ Using the 14n Rule. Orient J Chem 2015;31(3). |
| Copy the following to cite this URL: Kiremire E. M. A Unique Bypass to the Carbonyl Cluster ‘Nucleus’ Using the 14n Rule. Orient J Chem 2015;31(3). Available from: http://www.orientjchem.org/?p=10468 |
Introduction
Transition metal carbonyl clusters have stimulated immense interest for several decades largely due to their intriguing structural architecture, numerous potential industrial applications and challenging bonding properties. In this regard, the work by Wade and Mingos1-6as well as Jemmis7-8 has contributed tremendously towards the understanding of clusters. Subsequently, other research groups such as those headed by King, Teo, Zanello, and Slovokhotov 9-13 have expanded the knowledge especially on the large carbonyl clusters. The polyhedral skeletal electron pair theory (PSEPT) which uses mainly the 4n, 5n and 6n rules has classified clusters as closo, nido, arachno, hypho and some klapo. However on closer scrutiny of the structures and formulas of the simple boranes, hydrocarbons, carboranes and transition metal carbonyl clusters reveals that these clusters both simple and complex ones belong to a wide range of an infinite series. The series are formed according to definite numerical sequences reminiscent of the atomic number of elements.
Classification of Transition Metal Carbonyl Clusters Using the 14n Rule
The transition metal carbonyl clusters have been classified into closo, nido, arachno and hypho using Wade-Mingos rules for more than fifty years1. On closer analysis of the molecular structures of the clusters, it has been found that the transition metal carbonyl clusters form series based on 14n rule where n is the number of skeletal atoms that obey the 18 electron rule. A portion of the series is presented in Table 1 which will be used as a reference for classification purposes. Consequently, using the 14n rule as a BASIS, a given formula of a transition metal carbonyl cluster can readily be categorized. Some selected carbonyls have been used as illustrations of this simple and short method for categorizing carbonyl clusters.
Hypho Series(14n+8)
Consider the hypho cluster Os4(CO)1614; n = 4, 14n = 14×4 = 56, the total valence electrons(V) = 8×4+16×2 = 64. The difference between V = 64 and 14n = 56 is 64-56 = 8. Hence, we must add 8 to the value of 14n to have the same value of valence electrons. Therefore the series for this cluster may be written as T = 14n +8 (T = series symbol). Looking at Table 1, this cluster belongs to hypho series (H). The cluster number k is given by 2n-4 when n = number of skeletal atoms in the cluster. In this case, k =2n-4 = 2×4-4 = 4. For small clusters k also represents the number of linkages or bonds of the cluster atoms. Hence, this represents a square shown in S-9 of Scheme 1 tabulated below. The scheme shows common shapes found for two (M-2) to ten (M-10) transition metal skeletal elements in carbonyl clusters.
Table 1: Portion of Cluster Series for Main Group Elements and Transition Metal Carbonyl Clusters
| TRANSTION METAL CARBONYL CLUSTER SERIES(14n) | MAIN GROUP CLUSTER SERIES(4n) | k SERIES | REMARKS |
| 14n-10 | 4n-10 | 2n+5 | Hexacapped Series(C6C) |
| 14n-8 | 4n-8 | 2n+4 | Pentacapped Series (C5C) |
| 14n-6 | 4n-6 | 2n+3 | Tetracapped Series(C4C) |
| 14n-4 | 4n-4 | 2n+2 | Tricapped Series(C3C) |
| 14n-2 | 4n-2 | 2n+1 | Bicapped Series (C2C) |
| 14n | 4n | 2n | Monocapped Series(C1C) |
| 14n +2 | 4n+2 | 2n-1 | Closo Series(C) |
| 14n +4 | 4n+4 | 2n-2 | Nido Series(N) |
| 14n +6 | 4n+6 | 2n-3 | Arachno Series(A) |
| 14n +8 | 4n+8 | 2n-4 | Hypho Series(H) |
| 14n +10 | 4n+10 | 2n-5 | Klapo Series( H-1) |
Take another cluster, Os5(CO)19; n = 5, 14n = 14×5 =70, and the total valence electrons V = 5×8 + 19×2 = 78. We need to add 8 to the value of 14n in order to reach the value of 78. Therefore the cluster series can be expressed as T = 14n+8 = V. This means that Os5(CO)19 belongs to the same cluster series as Os4(CO)16. The k value for Os5(CO)19 is given by k= 2n-4 = 2×5 -4 = 6. It should be pointed out that from our previous work that the k value can be obtained15-16 from k = ½ (E-V), where E = 5×18 = 90 (sum of 18 electrons on the skeletal atoms assuming that each is surrounded by 18 electrons ) and V = 78 and thus k = ½ (90-78) = 6. This implies the 5 skeletal elements having 6 linkages which are found to be two triangles joined together at one of their corners as shown in the following sketch.
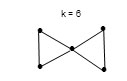
As can be seen the change in k value between the two clusters is 6-4 = 2 and the change in valence values is 78-64 = 14. Let us take examples from rhenium clusters. The case of Re4H4(CO)152― cluster, n = 4, 14n = 56, V = 7×4+4+15×2+2 = 64. This is similar to Os4(CO)16 case. Hence, T = 14n+8. This means the cluster belongs to hypho series and k = 4. This cluster was found to have a shape of a triangle with and extended arm indicated in S-10 in scheme 1. On the other hand, its isoelectronic analogue Re4H4(CO)16 has a square geometry(S-9) similar to that of Os4(CO)16 cluster. This means that in carbonyl clusters as in hydrocarbon clusters, there is some extent of k isomerism.
Arachno Series(14n+6)
The 14n rule is being applied mainly to known cases of clusters so the readership can verify that it readily gives the same results as those obtained by the well established methods. Let us illustrate it on Os2(CO)82― cluster; n =2, 14n = 14×2 =28, V = 8×2+8×2+2 = 34. Hence, T = 14n+6 =34. This means the cluster belongs to the arachno series (see Table 1). The cluster k value is given by k = 2n-3 = 2×2-3 = 1. This corresponds to the single bond that links the two osmium atoms(S-1). Take another cluster Os3(CO)12; n =3, 14n = 14×3 = 42 and V = 8×3+12×2 = 48. The cluster series T = 14n +6 = 48. This places Os3(CO)12 cluster as a member of arachno series with k = 2n-3 = 2×3-3 = 3. This means that the osmium atoms form a triangle(S-5). One of the next member in the series is Os4(CO)15; n = 4, 14n = 14×4 =56 and V = 8×4+15×2 = 62. Therefore T = 14n +6 = 62. Again, Os4(CO)15 is a member of the arachno series with k = 2n-3 = 2×4-3 = 5. This corresponds to five linkages of the four osmium atoms(S-11). The shape resembles a square with a diagonal. Let us take a cluster with six skeletal atoms, Os6(CO)17L4 [L = P(OMe)3]. In this case n = 6, 14n = 14×6 = 84 and V = 8×6+17×2+4×2 = 90. The cluster series will be given by T = 14n +6 = 90 =V. Therefore the cluster is a member of arachno series (see Table 1) with k value of 2n-3 = 2×6-3 = 9. Indeed the six osmium atoms form three linked triangles(S-21). If we use M to represent a skeletal atom, then the series go from M-2 to M-3, M-4, M-5, M-6 and so on. The corresponding change in M, k and V may be represented as M-2-1-34→M-3-3-48→M-4-5-62→M-5-7-76→M-5-9-90. The series can go on and on. The numerical change from one code to the next is simply (1, 2, 14). If we assume that M = osmium and all the ligands are CO, then the change from one cluster to the next is equivalent to adding an ‘Os(CO)3’ fragment. This fragment is loaded with 8+3×3 = 14 electron units. This also implies if we start with a given M-2 cluster in a series, we can construct an infinite number of hypothetical members that series.
Nido series(14n +4)
Let us consider the following osmium clusters14, Os3H2(CO)10; n = 3, 14n = 14×3 = 42, V = 8×3+2+10X2 = 46. Therefore T = 14n+4. This tells us, the cluster belongs to the nido series ( see Table 1) and k = 2n-2 = 2×3-2= 4. This could imply a triangular shape with a delocalized bond -8). If we take a next cluster of the series with four skeletal atoms such Os4(CO)14; n = 4, 14n =14×4 = 56 and V = 60 ,Then the cluster series becomes T = 14n+4 which belongs to the nido family. The k value will be 2n-2 = 2×4-2 = 6. This gives us a tetrahedral shape(S-12).
Closo Series (14n+2)
This is a type of clusters that follow the 14n+2 series in case of transition metal carbonyls while the main group elements obey the 4n+2 rule. However in this illustration we will focus only on the 14n+2 series. Let us consider the cluster Os5(CO)16; n = 5, 14n = 14×5 =70 and V = 8×5+16×2 = 72. Hence, T = 14n+2(see Table 1) and k = 2n-1 = 2×5-1 = 9. This value corresponds to the linkages observed in a trigonal bipyramid geometry(S-13). In actual fact, the skeletal shape of this cluster is a trigonal bipyramid14. It is also interesting to see that a similar result pertains in B5H52― when subjected to 4n rule. Thus, for B5H52― cluster; n = 5, 4n = 4×5 =20 and V =3×5+5+2 = 22. Hence, T = 4n+2 and k = 2n-1 = 2×5-1 = 9. The closo borane cluster B5H52― has a well known trigonal bipyramid shape15. In the case of the Os6(CO)182― an established octahedral geometry9 is well documented(S-19). Applying the 14n rule to the cluster, n = 6, 14n = 14×6 =84 and V = 8×6 +18×2+2 = 86. The cluster is clearly a member of the 14n+2 series. Accordingly, its cluster k value is 2n-1 = 2×6-1 = 11. The rhodium cluster, Rh6(CO)16 and Re6(C)(CO)192― which are known to have octahedral shape11 with V = 86 all belong to the 14n+2 series and have k value of 11. Corresponding to the 14n+2 series is the 4n+2 series of the main group elements. The closo borane cluster B6H62― with a regular octahedral geometry17 belongs to the 4n+2 series with k = 2n-1 = 2×6-1 = 11. This brings about a departure from correlating the k value with the number of connections or linkages of skeletal atoms. Thus, the k value may simply be regarded as a characteristic of a given cluster of particular series. In this case, for transition metal carbonyl clusters with six skeletal elements (M-6) and 86 valence electrons usually adopt an octahedral geometry and has a characteristic k value of 11. If we extrapolate below and above the k value of 11 for closo series, we will have the numbers such as 3, 5, 7,9,11 , 13, 15,17, 19, 21, … and so on. As can be seen, a movement across the same series from one cluster to another, the k value changes by 2. This observation is found in all series. It is interesting to note that for the series from closo to nido, arachno, hypho downwards, the value of valence electrons (V) is greater than that of 14n (V>14n), while for the mono-capped series (V = 14n) and for the closo capped series (V<14n).
Monocapped Series(14n)
This series (14n) is quite interesting in that when the number of the skeletal elements in the cluster in question are multiplied by 14, the resultant value is numerically the same as the number of valence electrons (V) of the cluster. Falling in this category is Os6(CO)18; n = 6, 14n =14×6 = 84, and V = 8×6+18×2 = 84. Thus 14n = V in value. Therefore, the cluster belongs to a series represented by T = 14n and it has a k value of 2n = 2×6 = 12. It is important to note that for this cluster, the k-value corresponds to the number of cluster linkages It has been found convenient to symbolize monocap with C1 and closo with C. Hence, the symbol for mono-capped series may be written as C1C. Since ‘monocap’ implies one of the skeletal atoms is being used for capping purposes, the rest of the atoms become the ‘inner’ closo system. In this case of Os6(CO)18 cluster, the capping is being done on the remaining 5 atoms which constitute a closo system presumably with a trigonal bipyramid geometry as has been observed9. We may also use the symbol C1C[M-5] to represent a mono-capping on a trigonal bipyramid geometry(S-18). Since capping involves a stepwise change of 12 valence electrons, if we remove them from 84 we will remain with 72 for the inner core. This corresponds to the equivalent presence of Os5(CO)16 inner core cluster. The inner core ‘Os5(CO)16’ belongs to the close series 14n+2. This also corresponds to the 4n+2 of the main group elements. Furthermore, if we subtract the equivalent of 10n from 14n+2 , the balance will be 4n+2 equivalent to a closo system of the main group element. That is to say, from 72 electrons of the inner core [M-5]of Os6(CO)18 cluster, if we deduct equivalent of 10n (10×5 =50) from 72 we will remain with 22 electrons. Indeed this is the electron count of B5H52―(22) which has a trigonal bipyramid geometry. The trigonal bipyramid geometry can be regarded as a capping on a tetrahedral geometry which in turn can be viewed as a capping on a trigonal planar shape. It is not surprising therefore that Os6(CO)18 cluster is regarded as a doubly capped tetrahedral shape9. Although the closo capping series start at T= 14n, the capping series can be extended to series such as nido and arachno. For instance start with Os3(CO)12, we can construct capping series by adding successive fragments of ‘Os(CO)2’ as follows, Os3(CO)12 → Os4(CO)14 → Os5(CO)16 → Os6(CO)18 → Os7(CO)20 → Os8(CO)22 and so on( ∆k =3). Hence, Os6(CO)18 is one member of the whole chain of (diagonal or vertical depending on how they are written)capping series. The next member of capping in this (horizontal)series(∆k = 2) of osmium clusters is Os7(CO)21 [ change involves Os(CO)3 fragment] where n =7, 14n = 14×7 = 98 and V = 8×7+21×2 = 98. Therefore, Os7(CO)21 is a member of mono-capped series with k =2n = 2×7 =14. Os7(CO)21 cluster may be viewed as a derivative of Os6(CO)18 by adding ‘Os(CO)3’ fragment. Since one of the skeletal atoms is utilized for capping, the ‘inner core’ of six is presumed to form a closo octahedral system. If we remove a capping fragment ‘Os(CO)2’ from Os7(CO)21 we will be left with ‘Os6(CO)19’. These chemical species are isoelectronic with the known Os6(CO)182― octahedral complex. Thus, Os7(CO)21 cluster is found to be a mono-capped octahedral complex14(S-23).The symbol C1C[M-6] may be used to represent this-meaning it is a mono-capped octahedral closo system. The cluster Re7(C)(CO)213― may be treated in the same way as Os7(CO)21 and it has a mono-capped octahedral geometry11.
Bi-capped Series (14n-2)
It has been observed that in bi-capped series and higher series, the value of 14n is numerically greater that of the valence electrons. That is, 14n > V for clusters symbolized as CnC where n = 2, 3, 4, 5, …). In the case of closo, nido, arachno, hypho and lower series, V>14n. The borderline is reached at mono-capped series(C1C) where V = 14n. In the bi-capped series, let us consider Re8(C)(CO)242―; n = 8, 14n = 14×8 = 112, V = 7×8+4+24×2+2 = 110. Therefore the series will be given by T = 14n-2 = V. In this series, the value of 14n exceeds that of valence electrons(V) by 2. This series will be in a higher row after the mono-capped series and a second row after the closo series row. Since 14n symbolizes a mono-capped (1 cap) series, any numerical multiple of (-2) will symbolize additional cap. Hence, the symbol 14n+1(-2) will correspond to a single cap C1 from the symbol 14n and an additional single cap C1 from 1(-2). Hence, the series T = 14n -2 will correspond to double-capped series C2C. In conclusion, the cluster Re8(C)(CO)242― is a member of a bi-capped series T = 14n-2 with k=2n+1 = 2.6-1 = 17. Since two of the atoms are involved in capping, the remaining 6 will be the ‘inner core’ of an octahedral system [M-6]. Thus, the eight skeletal atom (M-8) bi-capped cluster may be given the symbol C2C[M-6] and this means the Re8(C)(CO)242― cluster will be a bi-capped octahedron as is found experimentally11. The osmium cluster, Os8(CO)222― ; n = 8, 14n = 112, V = 8×8+22×2+2 = 110. Hence, T =14n-2. Again, this cluster is expected to be a bi-capped series based on an octahedral geometry as is observed9. Following the same approach, the clusters Ru8H2(CO)212―18, Os8H(CO)21―9, and Os8(C)(CO)21 belong to the bi-capped series(14n-2) based on an octahedral inner core and may be considered to have a similar structure. A possible bi-capped octahedral shape is shown in S-27 and S-28.
Tri-capped series(14n-4)
This is a series of clusters where the value of 14n exceeds that of the valence electrons (V) by 4. Take the example of Os9(CO)242―; n = 9, 14n = 14×9 = 126, V = 8×9+24×2+2 = 122. This gives us the series T= 14n-4 = V. The k value for this cluster will be 2n+2 = 2×9+2 = 20.To identify the capping, we can re-write the series as T= 14n+2(-2). If we use the symbol Cp to represent the capping, then in this case, Cp = C1 (implied from 14n) + C2 (implied from 2(-2). Thus, the overall capping can be represented as Cp = C3C. In this way, the symbol implies that 3 of the 9 skeletal atoms are being utilized for capping leaving the remaining six forming an octahedral ‘inner core’. Indeed, the Os9(CO)242― cluster is a tri- capped octahedron14 (S-29). Similar clusters such as Os9H(CO)24―14, Rh9(CO)193―21 and PtRh8(CO)192―20 can be analyzed in the same way and predicted as being tri-capped based on an octahedral inner core. In the case of capping, the value of k changes by 3 units. Since we are considering capping based on an octahedral unit (k =11), the mono-cap (C1C) will have k = 11+3 = 14, bi-cap(C2C) k = 11+3+3 = 17, and tri-cap(C3C) k = 11+3+3+3 = 20 and tetracap (C4C), k = 11+4×3 = 23.
Tetra-capped Series(14n-6)
Let us illustrate this starting with the cluster Ru10(C)(CO)242―; n = 10, 14n = 140 and V = 134. Hence, T = 14n-6 and may be written as T = 14n + 3(-2). The k value is given by k= 2n+3 = 2×10+3 = 23. In terms of capping, this will correspond to Cp = C1 + C3 = C4C. This implies that 4 atoms out 10 skeletal atoms are engaged in capping while the remaining six form the inner core of an octahedral geometry. This complex may be regarded to possess a tetra-capped octahedral geometry symbolized as C4C[M-6] and this has been observed11. This is sketched in S-30. By this approach of analysis the clusters Os10(CO)262―14, Os10(C)(CO)242―11, Os10H4(CO)242―14, and Rh10(CO)212― are expected to have a tetra-capped geometry based on an octahedral inner core. Furthermore, the k value of 23 can also be deduced from 11+3+3+3+3=23.
Selected higher capped series based on [M-6] inner core
Consider the cluster the palladium ruthenium carbonyl cluster19, Pd6Ru6(CO)242―. For this cluster n = 12, 14n = 14×12 = 168, V = 10×6+8×6+24×2+2 = 158. Hence, T = 14n-10 = 14n +5(-2). Therefore, this cluster belongs to the capping series Cp = C1+ C5 = C6C. This implies that this is a hexa-capped complex based on an octahedral inner core C6C [M-6] as is reported12,19. What is fascinating in this cluster, is the fact that the inner octahedral core comprises of the heavier Pd atoms. This is sketched in S-31. The cluster number k is given by 2n+5 = 2×12+5 = 29( 11+6×3). Since an octahedral geometry has 8 triangular faces, in principle, all of them could be capped. This is what is implied by the cluster, Os10(C)(CO)24Au(AuL)3, L = PPh3 ; where n =14, 14n = 14×14 = 196 and V = 8×10+4+24×2+11+(11+2)x3 = 182. The cluster series for the cluster will be T = 14n-14 = 14n+7(-2). The cluster will have a capping series Cp = C1+ C7 = C8C. This implies the cluster comprising of 14 skeletal atoms has 8 of them taking up capping positions while the remaining 6 constitute the inner core of an octahedral geometry, C8C [M-6]. Finally, let us consider the cluster Ni38Pt6(CO)48(H)5―; n = 44, 14n = 14×44 = 616 and V = 44×10+48×2+1+5 = 542. This cluster belongs to the series T = 14n-74 = 14n+37(-2). The capping series may be expressed as Cp = C1+C37 = C38C. This implies that the cluster has38 capping atoms based on an octahedral geometry of the inner core, C38C[M-6] and amazingly this is what is observed12. What is even more exciting is the fact that all the six inner core atoms comprise of the heavier Pt atoms. It is as if the heavier atoms sink towards the nuclear centre or inner layer and the lighter ones move towards the outer layers. This observation is similar to the case of Pd6Ru6(CO)242― cluster discussed above. Furthermore, the capping atoms on the outside the nuclear inner core must be capping on top of one another.
Possible Use in Data Interpretation
This method may also assist in the interpretation of some geometrical structures. For example, the set of clusters10, Ni5(CO)122―(T= 14n+6, k =7), Rh5(CO)15―( T = 14n+6, k =7), Rh5(CO)14I]2―( T = 14n +6, k =7), Ni3M2(CO)162―(M = Cr, Mo, W, T = 14n+6, k = 7), RuIr4(CO)152―( T = 14n+6, k = 7), and PtRh4(CO)142―( T = 14n+6, k = 7) were all reported to have elongated trigonal bipyramid structure whereas the second set of clusters10 Os5(CO)16( T = 14n+2, k = 9), and Os5(CO)152―( T = 14n+2, k = 9) were found to have a regular trigonal bipyramid shape. Clearly, the first set belong to the arachno series T = 14n+6 with the characteristic cluster number k =7 while the regular second set belong to the closo series T = 14n+2 with k = 9. These are expected to have a similar geometry as that of closo B5H52― which has a well documented regular trigonal bipyramid17. Since these two sets of clusters belong to different series, it is would probably be not possible to have identical characteristics.
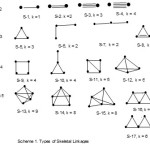 |
Scheme 1 Click here to View scheme |
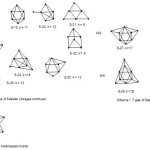 |
Scheme 1A Click here to View scheme |
This method of classifying carbonyl clusters may be portrayed as indicated in Scheme 2.
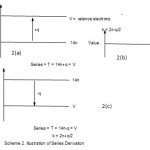 |
Scheme 2 Click here to View scheme |
In scheme 2(a), shows that V> 14n for Closo, Nido, Arachno, Hypho and Klapo Series. But the value of 14n increases in clusters until it is equal to V. This is shown in 2(b). That is, when 14n = V, the value of valence electrons, mono capping series (C1C) begin. In scheme 2(c), when the value of 14n becomes greater than V, that is 14n>V, then more capping series are generated. It is also found that when T = 14n +q, then the corresponding value cluster number is given by k =2n-q/2, while T = 14n, k = 2n and for T = 14n-q, the k value is 2n+q/2.
Conclusion
The formation of transition metal carbonyl clusters occurs in an ordered manner resulting into numerous series. The movement across a given series the cluster number varies by two cluster number units (∆k =2). In case of the osmium carbonyl clusters such change is equivalent to a formula change by ‘Os(CO)3’ fragment containing 14 electron units. On the other hand capping series involves the change in k value by 3 units(∆k =3). This is equivalent to a change in capping series by ‘Os(CO)2’. This fragment carries 12 valence electrons. Although the evolution of cluster series was demonstrated for those clusters whose inner core or nucleus is based on an implied octahedral closo geometry [M-6], this could also be done with other nuclear clusters such as [M-5]. [M-4], [M-8], and others. Equipped with this information, the construction of hypothetical cluster series of carbonyls becomes quite easy.
This method has been found to be reliable in the classification of carbonyl clusters in agreement with Wade-Mingos rules and it can also be used as a guide in predicting the geometries of wide range of small to medium type of clusters. With the concept of capping, this approach can give us a rough idea of how the cluster may geometrically appear to be based on its cluster molecular formula. The method involves deducing the cluster series of the complex from which the cluster number can be calculated and the type capping series based on the nuclear closo system. On reflecting on the capping, it appears to be a mechanism by which a cluster as it grows bigger and bigger a possible inner closo nuclear cluster may also be formed.
Acknowledgement
The author wishes to thank the University of Namibia and NAMSOV company, Namibia for financial support, and my wife, Merab Kambamu Kiremire for tremendous encouragement to write up this paper.
Dedication
The paper is dedicated to Prof. Charles Alfred Coulson who briefly but inspiringly taught the author as a student at Makerere University, Uganda, Africa, 1969, Prof. Irving Langmiur and Prof Gilbert Newton Lewis for their powerful insights of 18 and 8 electron rules respectively which they formulated more than 90 years ago.
References
- Wade, K. ,J. Chem. Soc., Dalton, 1971, 792-793.
- Mingos, D. M. P., Nature Physical Science, 1972, 236, 99-102.
- Welch, A. J., Chem. Comm., 2013, 49, 3615-3616.
- Wade, K., Adv. Inorg. Chem. Radiochem., 1976, 18, 1-66
- Mingos, D. M. P., Acc. Chem. Res., 1984, 17(9), 311-319.
- Mingos, D. M. P., Johnston, R. L., Struct. and Bonding, 1987, 68, 29-87
- Jemmis, E. D., J. Am. Chem. Soc., 2001, 123(18), 4313-4323.
- Jemmis, E. D., Balakrishnarajan, M. M.,Pattath, D., Chem. Rev, . 2002, 102(1), 93-144.
- King, R. B., Inorg. Chimica Acta, 1986, 116, 99-107.
- Teo, B. K., Longoni,G., Chung, F. R. K., Inorg. Chem., 1984, 23, 1257-1266.
- Zanello, P. in ‘Unusual Structures and Physical Properties’, Edited by Glein, M.,Gielen, M, Willen, R., Wrackmeyer, John Wiley and Sons, New York, 2002.
- Zanello, P., Rossi, F., Portugaliae Electrochimica Acta, 2011, 29(5), 309-327.
- Belyakova, O. A., Slovokhotov, Y. L., Russian Chemical Bulletin, International Edition, 2003, 52(11), 1-29.
- Hughes, A. K., Wade, K., Coord. Chem. Rev., 2000, 197, 191-229.
- Kiremire, E. M., Orient. J. Chem., 2015, 31(1), 293-302.
- Kiremire, E.M., Orient. J. Chem., 2014, 30(4), 1475-1485.
- Cotton, F. A., Wilkinson, G., ‘Advanced Inorganic Chemistry’, 4th Edition, John Wiley & Sons, New York, p317, 1980.
- Greenwood, N. N., Earnshaw, A., ‘Chemistry of the Elements’, 2nd Edition, Butterworth, Oxford, 1998.
- Martinengo, S., Fumagalli, A., Bonfichi, R., Ciani, G., J. Chem. Commun., 1982, 825-826.
- Pergola, R. D., Garlaschelli, L., J. Chem. Soc., Dalton, Trans., 1988, 201-205.
- Butcher, C. P. G., Dyson, P. J., Johnson, B. F. G., Khimyak, T., McIndoe, J. S., Chem., Eur., J. 2003, 9(4), 944-950.

This work is licensed under a Creative Commons Attribution 4.0 International License.









